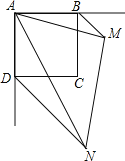
【题目】已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.
(1)求证:△ABM∽△NDA;
(2)连接BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
参考答案:
【答案】(1)证明见解析;(2)当∠BAM=22.5°时,四边形BMND为矩形,证明见解析.
【解析】分析:(1)由正方形ABCD,BM、DN分别是正方形的两个外角平分线,可证得∠ABM=∠ADN=135°,又由∠MAN=45°,可证得∠BAM=∠AND=45°-∠DAN,即可证得△ABM∽△NDA;(2)由四边形BMND为矩形,可得BM=DN,然后由△ABM∽△NDA,根据相似三角形的对应边成比例,可证得BM2=AB2,继而求得答案.
本题解析:(1)∵四边形ABCD是正方形,
∴∠DAB=∠ADC=∠ABC=90°,AB=AD.∵∠PAQ=45°∴∠1+∠2=45°,
∵ND平分∠FDC,MB平分∠EBC,∴∠EBM=∠FDN=45°,∴∠ABM=∠ADN=135°∠2+∠3=45° ,∴∠1=∠3 ∴△ABM∽△NDA
(2)当∠BAM=22.5°时,四边形BMND为矩形
理由:∵∠1=22.5°,∠EBM=45°∴∠4=22.5°,∴∠1=∠4,∴AB=BM
同理AD=DN∵AB=AD∴BM=DN ∵四边形ABCD是正方形∴∠ABD=∠ADB=45°
∴∠BDN=∠DBM=90°∴∠BDN+∠DBM=180°∴BM∥DN
∴四边形BMND为平行四边形
∵∠BDN=90°∴四边形BMND为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学课上,老师提出如下问题:
尺规作图:作一个角等于已知角
已知:∠AOB,
求作:∠A′OB′,使:∠A′OB′=∠AOB

小易同学作法如下:
①作射线O′A′;
②以点O为圆心,以任意长为半径作弧,交OA于C,交OB于D;
③以点O′为圆心,以OC长为半径作弧,交O′A于C
④以点C′圆心,以CD为半径作弧,交③中所画弧于D′;
⑤经过点D′作射线O′B′,∠A′O′B′就是所求的角.

老师说:“小易的作法正确”
请回答:小易的作图依据是______________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】南岗区某中学的王老师统计了本校九年一班学生参加体育达标测试的报名情况,并把统计的数据绘制成了不完整的条形统计图和扇形统计图.根据图中提供的数据回答下列问题:

(1)该学校九年一班参加体育达标测试的学生有多少人?
(2)补全条形统计图的空缺部分;
(3)若该年级有1200名学生,估计该年级参加仰卧起坐达标测试的有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l与直线l外一点P,求作:过点P且垂直于直线l的垂线a(尺规作图).
现给出一种作法,如下:
步骤一:在直线l外取一点E,以点P为圆心,以线段PE为半径画弧,交直线l于点M,N;
步骤二:分别以点M、N为圆心,大于
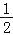 线段MN为半径画弧,过两弧的交点的直线a就是所求作的垂线.
线段MN为半径画弧,过两弧的交点的直线a就是所求作的垂线.(1)按上述操作步骤,请成功作出过点P且垂直于直线l的垂线a.(符合要求的一种图形),并说明理由.
(2)从你作图的过程中,思考要保证这种作法顺利作出,线段PE应该满足什么条件?
(3)为了避免这种情况产生,小明说只要在直线l上取点E好了,并给出了画法,画法对吗?请说明理由.
(作法:在直线l上取两点B、D,以P为圆心,以PD 为半径画圆交直线l于点E,以P为圆心,以PB 为半径画圆交直线l于点F,其中较小圆分别交PB,PF于点M、N,连接E、N和D、M,EN和MD相交于点H,则PH就是所求的垂线.)
(4)请在直线l上取点E,用直尺和圆规过点P且垂直于直线l的垂线a(与小明不同的方法,并要求尽可能简单).
-
科目: 来源: 题型:
查看答案和解析>>【题目】图a、图b是两张形状、大小完全相同的方格纸,方格纸中每个小正方形的边长为1,点A、B、D在小正方形的顶点上.
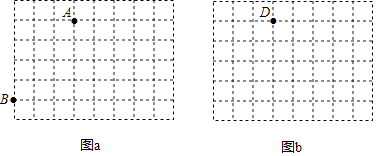
(1)在图a中画出△ABC(点C在小正方形顶点上),使△ABC是等腰三角形,且∠ABC=45°;
(2)在图b中画出△DEF(E、F在小正方形顶点上),使△DEF∽ABC且相似比为1: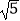 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某农庄计划在30亩空地上全部种植蔬菜和水果,菜农小张和果农小李分别承包了种植蔬菜和水果的任务.小张种植每亩蔬菜的工资y(元)与种植面积m(亩)之间的函数如图①所示,小李种植水果所得报酬z(元)与种植面积n(亩)之间函数关系如图②所示.
(1)如果种植蔬菜20亩,则小张种植每亩蔬菜的工资是 元,小张应得的工资总额是 元,此时,小李种植水果 亩,小李应得的报酬是 元;
(2)当10<n≤30时,求z与n之间的函数关系式;
(3)设农庄支付给小张和小李的总费用为w(元),当10<m≤30时,求w与m之间的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC≌△DEF,且△ABC的周长为12 cm,面积为6 cm2,则△DEF的周长为____cm,面积为_____cm2.
相关试题

