【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
(1)如图a,求证:△BCP≌△DCQ;
(2)如图,延长BP交直线DQ于点E.
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
参考答案:
【答案】
(1)证明:∵∠BCD=90°,∠PCQ=90°,
∴∠BCP=∠DCQ,
在△BCP和△DCQ中,
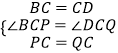 ,
,
∴△BCP≌△DCQ
(2)解:①如图b,∵△BCP≌△DCQ,
∴∠CBF=∠EDF,又∠BFC=∠DFE,
∴∠DEF=∠BCF=90°,
∴BE⊥DQ;
②∵△BCP为等边三角形,
∴∠BCP=60°,∴∠PCD=30°,又CP=CD,
∴∠CPD=∠CDP=75°,又∠BPC=60°,∠CDQ=60°,
∴∠EPD=45°,∠EDP=45°,
∴△DEP为等腰直角三角形.
【解析】(1)根据旋转的性质证明∠BCP=∠DCQ,得到△BCP≌△DCQ;(2)①根据全等的性质和对顶角相等即可得到答案;
②根据等边三角形的性质和旋转的性质求出∠EPD=45°,∠EDP=45°,判断△DEP的形状.
【考点精析】解答此题的关键在于理解旋转的性质的相关知识,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=
 x与双曲线y=
x与双曲线y=  (k>0)相交于A、B两点,且点A的横坐标为4.
(k>0)相交于A、B两点,且点A的横坐标为4. 
(1)求k的值;
(2)若双曲线y= (k>0)上一点C的纵坐标为8,求△AOC的面积;
(k>0)上一点C的纵坐标为8,求△AOC的面积;
(3)根据图象直接写出:当x取何值时,反比例函数的值大于一次函数的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】水温随时间的变化而变化,其中__________是自变量,__________是因变量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学计划组织九年级师生去韶山举行毕业联欢活动.下面是年级组长李老师和小芳、小明同学有关租车问题的对话:
李老师:“平安客运公司有60座和45座两种型号的客车可供租用,60座客车每辆每天的租金比45座的贵200元.”
小芳:“我们学校八年级师生昨天在这个客运公司租用4辆60座和2辆45座的客车到韶山参观,一天的租金共计5000元.”
小明:“我们九年级师生租用5辆60座和1辆45座的客车正好坐满.”
根据以上对话,解答下列问题:
(1)平安客运公司60座和45座的客车每辆每天的租金分别是多少元?
(2)按小明提出的租车方案,九年级师生到该公司租车一天,共需租金多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中:①
 =2
=2  ;②
;② 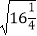 =4
=4  ;③
;③  ﹣
﹣  =
=  ;④
;④  =﹣2;⑤
=﹣2;⑤  =
=  ﹣
﹣  =1,其中正确的有( )
=1,其中正确的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】两条直线y=ax+b与y=bx+a在同一直角坐标系中的图象位置可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】江夏某村种植的水稻2010年平均亩产500kg,2012年平均亩产605kg,求该村亩产量的年平均增长率.
相关试题

