【题目】如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
实验与操作:根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)
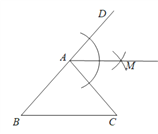
(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF
探究与猜想:若∠BAE=36°,求∠B的度数.

参考答案:
【答案】(1)见解析;(2)48°
【解析】试题分析:
(1)以点A为圆心,任意长为半径作弧交AD、AC于两点,再分别以这两点为圆心,大于这两点间的距离的一半为半径作弧,两弧交于一点M,过点M作射线AM,则射线AM为所求角平分线;
(2)分别以点A、C为圆心,大于AC的一半为半径作弧,两弧在AC的两侧各交于一点,过这两点作直线,角AM于点F,交BC于点E,则直线EF为AC的垂直平分线;连接CF,由已知条件先证∠CAM=∠ACB,再证△AOF≌△COE,由此可得OE=OF,从而可得四边形AECF是菱形,即可得到AE=CE,进一步可得∠EAC=∠ACB=∠B结合∠BAE=36°,结合三角形内角和定理即可得到∠B=![]() =48°.
=48°.
试题解析:
(1)如下图,图中射线AM为所求角平分线:
(2)如下图所示,直线EF为AC的垂直平分线,连接CF,
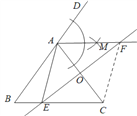
∵AB=AC,
∴∠ABC=∠ACB,
∵AM平分∠DAC,
∴∠DAM=∠CAM,
而∠DAC=∠ABC+∠ACB,
∴∠CAM=∠ACB,
∴EF垂直平分AC,
∴OA=OC,∠AOF=∠COE,
在△AOF和△COE中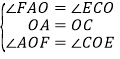 ,
,
∴△AOF≌△COE,
∴OF=OE,即AC和EF互相垂直平分,
∴四边形AECF的形状为菱形.
∴EA=EC,
∴∠EAC=∠ACB=∠B=![]() =48°,
=48°,
∴∠B=48°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC中,∠ABC=90°,AB=BC,点D是AC的中点,直角∠EDF的两边分别交AB、BC于点E、F,给出以下结论:①AE=BF;②S四边形BEDF=
 S△ABC;③△DEF是等腰直角三角形;④当∠EDF在△ABC内绕顶点D旋转时D旋转时(点E不与点A、B重合),∠BFE=∠CDF,上述结论始终成立的有( )个.
S△ABC;③△DEF是等腰直角三角形;④当∠EDF在△ABC内绕顶点D旋转时D旋转时(点E不与点A、B重合),∠BFE=∠CDF,上述结论始终成立的有( )个.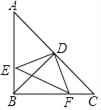
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )

A.0.324πm2
B.0.288πm2
C.1.08πm2
D.0.72πm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,图①是边长为1的等边三角形纸板,周长记为C1,沿图①的底边剪去一块边长为
 的等边三角形,得到图②,周长记为C2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的
的等边三角形,得到图②,周长记为C2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的 ),得图③④…,图n的周长记为Cn,若n≥3,则Cn-Cn-1=_____.
),得图③④…,图n的周长记为Cn,若n≥3,则Cn-Cn-1=_____.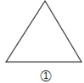



-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:把代数式x2﹣6x﹣7因式分解,可以如下分解:
x2﹣6x﹣7
=x2﹣6x+9﹣9﹣7
=(x﹣3)2﹣16
=(x﹣3+4)(x﹣3﹣4)
=(x+1)(x﹣7)
(1)探究:请你仿照上面的方法,把代数式x2﹣8x+7因式分解;
(2)拓展:把代数式x2+2xy﹣3y2因式分解:
当
 ________________时,代数式x2+2xy﹣3y2=0.
________________时,代数式x2+2xy﹣3y2=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个长方形运动场被分隔成
 、
、 、
、 、
、 、
、 共
共 个区,
个区,  区是边长为
区是边长为 的正方形,
的正方形,  区是边长为
区是边长为 的正方形.
的正方形.(1)列式表示每个
 区长方形场地的周长,并将式子化简;
区长方形场地的周长,并将式子化简;(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果
 ,
,  ,求整个长方形运动场的面积.
,求整个长方形运动场的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子错误的是( )
A.cos40°=sin50°
B.tan15°tan75°=1
C.sin225°+cos225°=1
D.sin60°=2sin30°
相关试题

