【题目】如图,因为AB∥CD(已知),所以∠BEF=∠CFE(两直线平行,) 因为EG平分∠BEF,FH平分∠CFE(已知),
所以∠2= ![]() ∠BEF,∠3=()
∠BEF,∠3=()
所以∠2=(等量代换),
所以EG∥( , 两直线平行).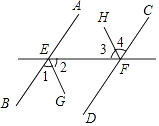
参考答案:
【答案】内错角相等;![]() ∠CFE;角平分线定义;∠3;FH;内错角相等
∠CFE;角平分线定义;∠3;FH;内错角相等
【解析】解:因为AB∥CD(已知),所以∠BEF=∠CFE(两直线平行,内错角相等), 因为EG平分∠BEF,FH平分∠CFE(已知),
所以∠2= ![]() ∠BEF,∠3=
∠BEF,∠3= ![]() ∠CFE(角平分线定义),
∠CFE(角平分线定义),
所以∠2=∠3(等量代换),
所以EG∥FH(内错角相等,两直线平行).
所以答案是:内错角相等; ![]() ∠CFE;角平分线定义;∠3;FH;内错角相等.
∠CFE;角平分线定义;∠3;FH;内错角相等.
【考点精析】认真审题,首先需要了解平行线的判定与性质(由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小华家距离县城15km,星期天8:00,小华骑自行车从家出发,到县城购买学习用品,小华与县城的距离y(km)与骑车时间x(h)之间的关系如图所示,给出以下结论:①小华骑车到县城的速度是15km/h;②小华骑车从县城回家的速度是13km/h;③小华在县城购买学习用品用了1h;④B点表示经过
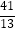 h,小华与县城的距离为15km(即小华回到家中),其中正确的结论有( )
h,小华与县城的距离为15km(即小华回到家中),其中正确的结论有( ) 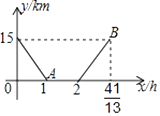
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,∠F=60°,求:
(1)指出旋转中心和旋转角度;
(2)求DE的长度和∠EBD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了求1+2+22+23+24+…+22018的值,可以设s=1+2+22+23+…+22018 , 则则2s=2+22+23+24+…+22018 , 所以2s﹣s=22019﹣1,即1+2+22+…+22018=22019﹣1,仿照以上推理,计算出1+7+72+73+…72020的值( )
A.72021﹣1
B.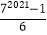
C.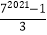
D.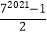
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位A,B,C,D四人随机分成两组赴北京,上海学习,每组两人.
(1)求A去北京的概率;
(2)用列表法(或树状图法)求A,B都去北京的概率;
(3)求A,B分在同一组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2-4x+5的顶点坐标是( )
A.(-2,1)B.(2,1)C.(-2,-1)D.(2,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.(a+b)2=a2+b2
B.a8÷a4=a2
C.2a+3b=5ab
D.a2a3=a5
相关试题

