【题目】我们把a、b两个数中较小的数记作min{a,b},直线y=kx﹣k﹣2(k<0)与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点,则k的取值为
参考答案:
【答案】2﹣2 ![]() 或﹣
或﹣ ![]() 或﹣1
或﹣1
【解析】解:根据题意,x2﹣1<﹣x+1,即x2+x﹣2<0,
解得:﹣2<x<1,
故当﹣2<x<1时,y=x2﹣1;
当x≤﹣2或x≥1时,y=﹣x+1;
函数图象如下:
由图象可知,∵直线y=kx﹣k﹣2(k<0)与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点,且k<0,
①直线y=kx﹣k﹣2经过点(﹣2,3)时,3=﹣2k﹣k﹣2,k=﹣ ![]() ,此时直线y=﹣
,此时直线y=﹣ ![]() x﹣
x﹣ ![]() ,与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点.
,与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点.
②直线y=kx﹣k﹣2与函数y=x2﹣1相切时,由 ![]() 消去y得x2﹣kx+k+1=0,∵△=0,k<0,
消去y得x2﹣kx+k+1=0,∵△=0,k<0,
∴k2﹣4k﹣4=0,
∴k=2﹣2 ![]() (或2+2
(或2+2 ![]() 舍弃),此时直线y=(2﹣2
舍弃),此时直线y=(2﹣2 ![]() )x﹣4+2
)x﹣4+2 ![]() 与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点.
与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点.
③直线y=kx﹣k﹣2和直线y=﹣x+1平行,k=﹣1,直线为y=﹣x﹣1与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点.
综上,k=2﹣2 ![]() 或﹣
或﹣ ![]() 或﹣1.
或﹣1.
故答案为:2﹣2 ![]() 或﹣
或﹣ ![]() 或﹣1.
或﹣1.
结合x的范围画出函数y=min{x2﹣1、﹣x+1}图象,由直线y=kx﹣k﹣2(k<0)与该函数图象只有两个交点且k<0,判断直线的位置得①直线y=kx﹣k﹣2经过点(﹣2,3)时可以求出k;②直线y=kx﹣k﹣2与函数y=x2﹣1相切时,可以求出k.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一圆的半径是10cm,圆内的两条平行弦长分别为12cm和16cm,则这两条平行弦之间的距离为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=
 cm,∠BAC=120°,点P在BC上从C向B运动,点Q在AB、AC上沿B→A→C运动,点P、Q分别从点C、B同时出发,速度均为1cm/s,当其中一点到达终点时两点同时停止运动,则当运动时间t=_____s时,△PAQ为直角三角形.
cm,∠BAC=120°,点P在BC上从C向B运动,点Q在AB、AC上沿B→A→C运动,点P、Q分别从点C、B同时出发,速度均为1cm/s,当其中一点到达终点时两点同时停止运动,则当运动时间t=_____s时,△PAQ为直角三角形.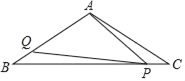
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)①若
 有意义,则化简
有意义,则化简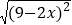 = .
= .②化简:a2
 = .
= .(2)已知|7﹣9m|+(n﹣3)2=9m﹣7﹣
 ,求(n﹣m)2018.
,求(n﹣m)2018. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在菱形ABCD中,∠ABC=60°,M、N分别是边BC,CD上的两个动点,∠MAN=60°,AM、AN分别交BD于E、F两点.

(1)如图1,求证:CM+CN=BC;
(2)如图2,过点E作EG∥AN交DC延长线于点G,求证:EG=EA;
(3)如图3,若AB=1,∠AED=45°,直接写出EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1、x2是一元二次方程2x2﹣2x+1﹣3m=0的两个实数根,且x1、x2满足不等式x1x2+2(x1+x2)>0,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)①画出△ABC关于y轴对称的△A1B1C1;
②画出△ABC关于原点O成中心对称的△A2B2C2;
(2)求△A2B2C2的面积.
相关试题

