【题目】已知x1、x2是一元二次方程2x2﹣2x+1﹣3m=0的两个实数根,且x1、x2满足不等式x1x2+2(x1+x2)>0,求实数m的取值范围.
参考答案:
【答案】解:∵方程2x2﹣2x+1﹣3m=0有两个实数根,
∴△=4﹣8(1﹣3m)≥0,解得m≥ ![]() .
.
由根与系数的关系,得x1+x2=1,x1x2= ![]() .
.
∵x1x2+2(x1+x2)>0,
∴ ![]() +2>0,解得m<
+2>0,解得m< ![]() .
.
∴ ![]() ≤m<
≤m< ![]()
【解析】已知x1、x2是一元二次方程2x2﹣2x+1﹣3m=0的两个实数根,可推出△=(﹣2)2﹣4×2(1﹣3m)≥0,根据根与系数的关系可得x1x2= ![]() ,x1+x2=1;且x1、x2满足不等式x1x2+2(x1+x2)>0,代入即可得到一个关于m的不等式,由此可解得m的取值范围.
,x1+x2=1;且x1、x2满足不等式x1x2+2(x1+x2)>0,代入即可得到一个关于m的不等式,由此可解得m的取值范围.
【考点精析】掌握求根公式和根与系数的关系是解答本题的根本,需要知道根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)①若
 有意义,则化简
有意义,则化简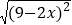 = .
= .②化简:a2
 = .
= .(2)已知|7﹣9m|+(n﹣3)2=9m﹣7﹣
 ,求(n﹣m)2018.
,求(n﹣m)2018. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们把a、b两个数中较小的数记作min{a,b},直线y=kx﹣k﹣2(k<0)与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点,则k的取值为
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在菱形ABCD中,∠ABC=60°,M、N分别是边BC,CD上的两个动点,∠MAN=60°,AM、AN分别交BD于E、F两点.

(1)如图1,求证:CM+CN=BC;
(2)如图2,过点E作EG∥AN交DC延长线于点G,求证:EG=EA;
(3)如图3,若AB=1,∠AED=45°,直接写出EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)①画出△ABC关于y轴对称的△A1B1C1;
②画出△ABC关于原点O成中心对称的△A2B2C2;
(2)求△A2B2C2的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在直角坐标系中,A(0,3),B(3,0),点D为射线OB上一动点(D不与O、B重合),以AD为边在AD右侧作正方形ADEF,连BF、AE相交于点G.

(1)若点D坐标为(a2+
 ,0),且a+
,0),且a+ ,求F点坐标;
,求F点坐标;(2)在(1)的条件下,求AG的长;
(3)如图2,当D点在线段OB延长线上时,若BD:BF=14,求BG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】进入冬季,我市空气质量下降,多次出现雾霾天气.商场根据市民健康需要,代理销售一种防尘口罩,进货价为20元/包,经市场销售发现:销售单价为30元/包时,每周可售出200包,每涨价1元,就少售出5包.若供货厂家规定市场价不得低于30元/包,且商场每周完成不少于150包的销售任务.
(1)试确定周销售量y(包)与售价x(元/包)之间的函数关系式;
(2)试确定商场每周销售这种防尘口罩所获得的利润w(元)与售价x(元/包)之间的函数关系式,并直接写出售价x的范围;
(3)当售价x(元/包)定为多少元时,商场每周销售这种防尘口罩所获得的利润w(元)最大?最大利润是多少?
相关试题

