【题目】已知二次函数![]() (
(![]() 是常数).
是常数).
(1)求证:不论![]() 为何值,该函数的图象与x轴没有公共点;
为何值,该函数的图象与x轴没有公共点;
(2)把该函数的图象沿![]() 轴向下平移多少个单位长度后,得到的函数的图象与
轴向下平移多少个单位长度后,得到的函数的图象与![]() 轴只有一个公共点?
轴只有一个公共点?
参考答案:
【答案】(1)、证明过程见解析;(2)、3.
【解析】
试题分析:(1)、利用根的判别式进行说明;(2)、将函数化成顶点式,然后进行说明.
试题解析:(1)、∵△=(﹣2m)2﹣4×1×(m2+3)=4m2﹣4m2﹣12=﹣12<0
∴方程x2﹣2mx+m2+3=0没有实数解, 即不论m为何值,该函数的图象与x轴没有公共点;
(2)、y=x2﹣2mx+m2+3=(x﹣m)2+3,
∴把函数y=x2﹣2mx+m2+3的图象沿y轴向下平移3个单位长度后,得到的函数的图象与x轴只有一个公共点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个小球向斜上方抛出,它的行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=﹣x2+4x+1,则小球能到达的最大高度是m.
-
科目: 来源: 题型:
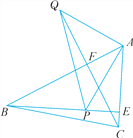
查看答案和解析>>【题目】如图,已知在△ABC中,AB>AC,BE,CF都是△ABC的高线,P是BE上一点,且BP=AC,Q是CF延长线上一点,且CQ=AB,连结AP,AQ,QP.求证:
(1)AQ=PA.
(2)AP⊥AQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a-b=2019,c+d=2018,则 (b+c)-(a-d ) 的值是___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正三角形、平行四边形、矩形、菱形、正方形中,不是中心对称图形的是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.

求证:(1)△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若正数a的平方根为x和2x﹣6,则a=_____.
相关试题

