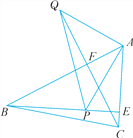
【题目】如图,已知在△ABC中,AB>AC,BE,CF都是△ABC的高线,P是BE上一点,且BP=AC,Q是CF延长线上一点,且CQ=AB,连结AP,AQ,QP.求证:
(1)AQ=PA.
(2)AP⊥AQ.
参考答案:
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)由已知条件可求出∠ABP=∠QCA,即可根据SAS证得△AQC≌△PAB(SAS),就可以得出AP=AQ;
(2)根据全等三角形的性质,由△AQC≌△PAB可得出∠BAP=∠CQA,再由∠CQA+∠FAQ=90°,即可证明.
试题解析:(1)∵BE,CF是△ABC的高线,
∴BE⊥AC,CF⊥AB,
∴∠ABP+∠BAC=∠ACQ+∠BAC=90°,
∴∠ABP=∠ACQ.
在△AQC和△PAB中,∵ 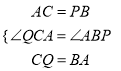
∴△AQC≌△PAB(SAS).∴AQ=PA.
(2)∵△AQC≌△PAB,∴∠BAP=∠CQA.
∵∠CQA+∠BAQ=90°,
∴∠BAP+∠BAQ=90°,∴AP⊥AQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级某班同学在庆祝2015年元旦晚会上进行抽奖活动.在一个不透明的口袋中有三个完全相同的小球,把它们分别标号1、2、3.随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号.
(1)请用列表或画树形图的方法(只选其中一种),表示两次摸出小球上的标号的所有结果;
(2)规定当两次摸出的小球标号相同时中奖,求中奖的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=4,AD=6,延长BC到点E,使CE=2,连结DE,动点P从点B出发,以每秒2个单位的速度沿BC→CD→DA向终点A运动,设点P的运动时间为t(s),当t为何值时,△ABP和△DCE全等?

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个小球向斜上方抛出,它的行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=﹣x2+4x+1,则小球能到达的最大高度是m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a-b=2019,c+d=2018,则 (b+c)-(a-d ) 的值是___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 (
( 是常数).
是常数).(1)求证:不论
 为何值,该函数的图象与x轴没有公共点;
为何值,该函数的图象与x轴没有公共点;(2)把该函数的图象沿
 轴向下平移多少个单位长度后,得到的函数的图象与
轴向下平移多少个单位长度后,得到的函数的图象与 轴只有一个公共点?
轴只有一个公共点? -
科目: 来源: 题型:
查看答案和解析>>【题目】在正三角形、平行四边形、矩形、菱形、正方形中,不是中心对称图形的是 .
相关试题

