搜索
【题目】下列四组数中不是勾股数的一组是（ ）
A. 4，5，6 B. 7，24，25 C. 5，12，13 D. 11，60，61
参考答案：
【答案】A
【解析】
欲判断是否为勾股数组，必须根据勾股数是正整数，同时还需验证两小边的平方和是否等于最长边的平方．
A. ∵42+52≠62，∴ 4，5，6不是勾股数组；
B. ∵72+242=252，∴7，24，25是勾股数组；
C. ∵52+122=132，∴5，12，13是勾股数组；
D. ∵112+602=612，∴11，60，61是勾股数组；
故选A.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）作△ABC的外接圆；
（2）若AC=BC，AB=8，C到AB的距离是2，求△ABC的外接圆半径．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一个多边形的各个内角与它的某个外角的和是2036，求:这个多边形的边数和这个外角的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】九(1)班数学兴趣小组经过市场调查，整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表：
时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200－2x
已知该商品的进价为每件30元，设销售该商品每天的利润为y元。
(1)求出y与x的函数关系式；
(2)问销售该商品第几天时，当天的销售利润最大？最大利润是多少？
(3)该商品在销售过程中，共有多少天每天的销售利润不低于4800元？请直接写出结果。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
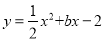与x轴交于A、B两点，与y轴交于C点，且A（﹣1，0）．
（1）求抛物线的解析式及顶点D的坐标；
（2）判断△ABC的形状，证明你的结论；
（3）点M是抛物线对称轴上的一个动点，当CM+AM的值最小时，求M的坐标；
（4）在线段BC下方的抛物线上有一动点P，求△PBC面积的最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算 x 2 y 2 _______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC为等边三角形，AE=CD，AD、BE相交于点P，BQ⊥AD于Q，PQ=4，PE=1．
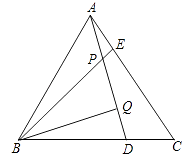
（1）求证：∠BPQ=60°（提示：利用三角形全等、外角的性质）
（2）求BE的长．
相关试题
