【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
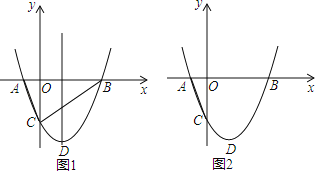
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当CM+AM的值最小时,求M的坐标;
(4)在线段BC下方的抛物线上有一动点P,求△PBC面积的最大值.
参考答案:
【答案】(1)抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣2,顶点D的坐标是(
x﹣2,顶点D的坐标是(![]() ,﹣
,﹣![]() );
);
(2)△ABC是直角三角形,理由见解析;
(3)点M的坐标为(![]() ,
,![]() );
);
(4)△PBC面积的最大值是4.
【解析】试题分析:(1)把点A的坐标代入函数解析式来求b的值;然后把函数解析式转化为顶点式,即可得到点D的坐标;(2)由两点间的距离公式分别求出AC,BC,AB的长,再根据勾股定理即可判断出△ABC的形状;(3)根据抛物线的性质可得点A与点B关于对称轴x=![]() 对称,求出点B,C的坐标,根据轴对称性,可得MA=MB,两点之间线段最短可知,MC+MB的值最小.则BC与直线x=
对称,求出点B,C的坐标,根据轴对称性,可得MA=MB,两点之间线段最短可知,MC+MB的值最小.则BC与直线x=![]() 交点即为M点,利用得到系数法求出直线BC的解析式,即可得到点M的坐标.(4)过点P作y轴的平行线交BC于F.利用待定系数法求得直线BC的解析式,可求得点F的坐标,设P点的横坐标为m,可得点P的纵坐标,继而可得线段PF的长,然后利用面积和即S△PBC=S△CPF+S△BPF=
交点即为M点,利用得到系数法求出直线BC的解析式,即可得到点M的坐标.(4)过点P作y轴的平行线交BC于F.利用待定系数法求得直线BC的解析式,可求得点F的坐标,设P点的横坐标为m,可得点P的纵坐标,继而可得线段PF的长,然后利用面积和即S△PBC=S△CPF+S△BPF=![]() PF×BO,即可求出.
PF×BO,即可求出.
试题解析:(1)把A(﹣1,0)代入![]() 得到:0=
得到:0=![]() ×(﹣1)2﹣b﹣2,
×(﹣1)2﹣b﹣2,
解得b=﹣![]() ,
,
则该抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣2.
x﹣2.
又∵y=![]() x2﹣
x2﹣![]() x﹣2=
x﹣2=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() ,
,
∴顶点D的坐标是(![]() ,﹣
,﹣![]() );
);
(2)由(1)知,该抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣2.则C(0,﹣2).
x﹣2.则C(0,﹣2).
又∵y=![]() x2﹣
x2﹣![]() x﹣2=
x﹣2=![]() (x+1)(x﹣4),
(x+1)(x﹣4),
∴A(﹣1,0),B(4,0),
∴AC=![]() ,BC=2
,BC=2![]() ,AB=5,
,AB=5,
∴AC2+BC2=AB2,
∴△ABC是直角三角形;
(3)∵顶点D的坐标为(![]() ,
, ![]() ),
),
∴抛物线的对称轴为x=![]() ,
,
∵抛物线y=![]() x2+bx2与x轴交于A,B两点,
x2+bx2与x轴交于A,B两点,
∴点A与点B关于对称轴x=![]() 对称,
对称,
∵A(1,0).
∴点B的坐标为(4,0),
当x=0时,y=![]() x2
x2![]() x2=2,
x2=2,
则点C的坐标为(0,2),
则BC与直线x=![]() 交点即为M点,如图,
交点即为M点,如图,
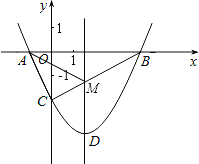
根据轴对称性,可得MA=MB,两点之间线段最短可知,MC+MB的值最小。
设直线BC的解析式为y=kx+b,
把C(0,2),B(4,0)代入,可得![]() ,
,
解得:  ,
,
∴y=![]() x2,
x2,
当x=![]() 时,y=
时,y=![]() ×
×![]() 2=54,
2=54,
∴点M的坐标为(![]() ,
,![]() ).
).
(4)如答图2,过点P作y轴的平行线交BC于F.
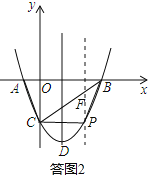
设直线BC的解析式为y=kx﹣2(k≠0).
把B(4,0)代入,得
0=4k﹣2,
解得k=![]() .
.
故直线BC的解析式为:y=![]() x﹣2.
x﹣2.
故设P(m, ![]() m2﹣
m2﹣![]() m﹣2),则F(m,
m﹣2),则F(m, ![]() m﹣2),
m﹣2),
∴S△PBC=![]() PFOB=
PFOB=![]() ×(
×(![]() m﹣2﹣
m﹣2﹣![]() m2+
m2+![]() m+2)×4=﹣(m﹣2)2+4,
m+2)×4=﹣(m﹣2)2+4,
即S△PBC=﹣(m﹣2)2+4,
∴当m=2时,△PBC面积的最大值是4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多边形的各个内角与它的某个外角的和是2036,求:这个多边形的边数和这个外角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200-2x
已知该商品的进价为每件30元,设销售该商品每天的利润为y元。
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?最大利润是多少?
(3)该商品在销售过程中,共有多少天每天的销售利润不低于4800元?请直接写出结果。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四组数中不是勾股数的一组是( )
A. 4,5,6 B. 7,24,25 C. 5,12,13 D. 11,60,61
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算 x 2 y 2 _______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=4,PE=1.
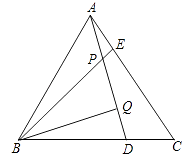
(1)求证:∠BPQ=60°(提示:利用三角形全等、外角的性质)
(2)求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的一个角为70゜,则其顶角的度数为_____ .
相关试题

