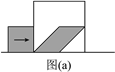
【题目】已知大正方形的边长为4厘米,小正方形的边长为2厘米,起始状态如图所示,大正方形固定不动,把小正方形以1厘米∕秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.完成下列问题:
(1)平移1.5秒时,S为________平方厘米;
(2)当2≤t≤4时,求小正方形的一条对角线扫过的图形的面积;
(3)当S为2平方厘米时,求小正方形平移的距离.

参考答案:
【答案】(1)3 (2)4![]() (3)1厘米或5厘米
(3)1厘米或5厘米
【解析】
(1)1.5秒时,小正方形向右移动1.5厘米,即可计算出重叠部分面积;
(2)画出图形,计算所得图形面积即可;
(3)小正方形的高不变,根据面积即可求出小正方形平移的距离.
(1) 1.5秒时,小正方形向右移动1.5厘米,S=2×1.5=3平方厘米;
(2)如图(a)所示,小正方形的一条对角线扫过的面积为图中平行四边形的面积,
面积为2×2=4(厘米2).
(3)当S为2平方厘米时,重叠部分的宽为2÷2=1(厘米),
①如图(b),小正方形平移的距离为1厘米;

②如图(c),小正方形平移的距离为4+1=5(厘米).

故小正方形平移的距离为1厘米或5厘米.
-
科目: 来源: 题型:
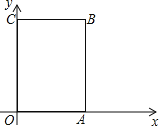
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动(即:沿着长方形移动一周)
(1)写出点B的坐标( , );
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴距离为4个单位长度时,求点P移动的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把△ABC平移至点A′的位置,使点A与点A′对应,画出平移后得到的△A′B′C′;
(2)△A′B′C′可以看成是把△ABC如何平移得到的?
(3)写出图中与线段AA′平行且相等的线段(可用字母表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10 ,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.
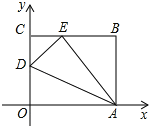
(1)求CE和OD的长;
(2)求直线DE的表达式;
(3)直线y=kx+b与DE平行,当它与矩形OABC有公共点时,直接写出b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠ACD是△ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG∥CE,交AB于点G,若∠1=70°,∠2=30°,则∠3的度数为( )

A. 30° B. 40° C. 45° D. 50°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知A(
 ,y1),B(2,y2)为反比例函数y=
,y1),B(2,y2)为反比例函数y= 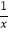 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )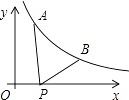
A.( ,0)
,0)
B.(1,0)
C.( ,0)
,0)
D.( ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知α是锐角,且点A(
 ,a),B(sin30°+cos30°,b),C(﹣m2+2m﹣2,c)都在二次函数y=﹣x2+x+3的图象上,那么a、b、c的大小关系是( )
,a),B(sin30°+cos30°,b),C(﹣m2+2m﹣2,c)都在二次函数y=﹣x2+x+3的图象上,那么a、b、c的大小关系是( )
A.a<b<c
B.a<c<b
C.b<c<a
D.c<b<a
相关试题

