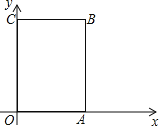
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动(即:沿着长方形移动一周)
(1)写出点B的坐标( , );
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴距离为4个单位长度时,求点P移动的时间.
参考答案:
【答案】(1)点B的坐标(4,5);(2)点P的坐标为BC边中点(3,5);(3)当点P移动2秒或5秒时,点P到x轴的距离为4个单位长度
【解析】
(1)根据长方形的性质,易得P的坐标;
(2)根据题意,P的运动速度与移动的时间,可得P运动了8个单位,进而结合长方形的长与宽可得答案;
(3)根据题意,当点P到x轴距离为4个单位长度时,有P在AB与OC上两种情况,分别求解可得答案.
解:(1)点B的坐标(4,5),故答案为:4,5;
(2)当点P移动了4秒时,点P移动了4×2=8个单位长度,
∵C点的坐标为(0,5),
∴OC=5,
∴85=3,
∴此时,点P的位置在线段BC上,且CP=3,
如图所示,点P的坐标为BC边中点(3,5).
(3)当点P在OC上时,OP=4,
此时所用时间为4÷2=2(s);
当点P在AB上时,AP=4,BP=1,
∵A点的坐标为(4,0)
∴OA=CB=4,
∵C点的坐标为(0,5)
∴OC=5,OC+CB+BP=5+4+1=10,此时所用时间为10÷2=5(s);
综上所述,当点P移动2秒或5秒时,点P到x轴的距离为4个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班抽取6名同学参加体能测试,成绩如下:85,95,85,80,80,85.下列表述错误是( )
A.众数是85
B.平均数是85
C.方差是20
D.极差是15 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B.
(1)求一次函数的解析式;
(2)判断点C(4,-2)是否在该一次函数的图象上,说明理由;
(3)若该一次函数的图象与x轴交于D点,求△BOD的面积.

-
科目: 来源: 题型:
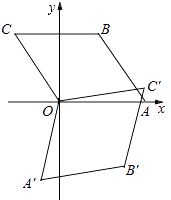
查看答案和解析>>【题目】如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )
A.(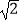 ,﹣
,﹣ 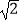 )
)
B.(﹣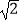 ,
, 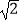 )
)
C.(2,﹣2)
D.(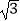 ,﹣
,﹣ 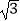 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把△ABC平移至点A′的位置,使点A与点A′对应,画出平移后得到的△A′B′C′;
(2)△A′B′C′可以看成是把△ABC如何平移得到的?
(3)写出图中与线段AA′平行且相等的线段(可用字母表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10 ,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.
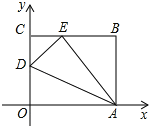
(1)求CE和OD的长;
(2)求直线DE的表达式;
(3)直线y=kx+b与DE平行,当它与矩形OABC有公共点时,直接写出b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知大正方形的边长为4厘米,小正方形的边长为2厘米,起始状态如图所示,大正方形固定不动,把小正方形以1厘米∕秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.完成下列问题:
(1)平移1.5秒时,S为________平方厘米;
(2)当2≤t≤4时,求小正方形的一条对角线扫过的图形的面积;
(3)当S为2平方厘米时,求小正方形平移的距离.

相关试题

