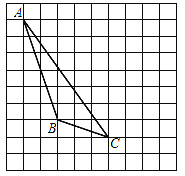
【题目】如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
(1)画出△A′B′C′;
(2)利用网格点和直尺画图:画出AB边上的高线CD;
(3)图中△ABC的面积是 ;
(4)△ABC与△EBC面积相等,点E是异于A点的格点,则这样的E点有 个.
参考答案:
【答案】(1)画图见解析;(2)画图见解析;(3)图中△ABC的面积是8;
(4)这样的E点有3个.
【解析】试题分析: (1)根据网格结构找出点A、B、C向右平移4个单位的对应点A′、B′、C′的位置,然后顺次连接即可;
(2)根据网格结构与高线的定义作出即可;
(3)根据底×高÷2计算得出.
(4)根据等底等高的三角形的面积相等过点A作BC的平行线,经过的格点即为所求.
试题解析:
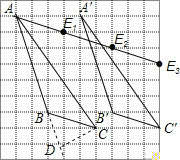
(1)如图所示;
(2)高线CD如图所示;
(3)图中△ABC的面积是8;
(4)△ABC与△EBC面积相等,点E是异于A点的格点,格点E如图所示则这样的E点有 3个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=(m﹣1)x的图象上两点A(x1,y1),B(x2,y2),当x1<x2时,有y1>y2,那么m的取值范围是( )
A. m<1B. m>1C. m<2D. m>0
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题4分)(1)在图1中, 求∠A1+∠B1+∠C1+∠A2+∠B2+∠C2的度数= .
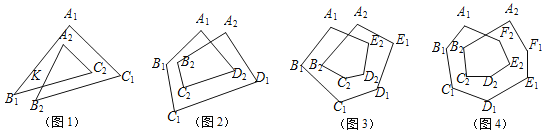
(2)我们作如下规定:
图1称为2环三角形,它的内角和为∠A1+∠B1+∠C1+∠A2+∠B2+∠C2;
图2为2环四边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠A2+∠B2+∠C2+∠D2;
图3称为2环5五边形,它的内角和为∠A1+∠B1+∠C1+∠D1+∠E1+∠A2+∠B2+∠C2+∠D2+∠E2;
想一想:2环n边形的内角和为 度(只要求直接写出结论).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)求∠AFE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个粒子在第一象限内及x轴、y轴上运动,在第一分钟内它从原点运动到(1,0),而后它接着按图示在x轴、y轴平行的方向上来回运动,且每分钟移动一个长度单位,那么在2015分钟后这个粒子所处的位置(坐标)是 ______ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,是必然事件的是( )
A. 掷一块石块,石块下落
B. 射击运动员射击一次,命中10环
C. 随意掷一块质地均匀的骰子,掷出的点数是1
D. 在一个装满白球和黑球的袋中摸球,摸出红球
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(2,﹣12)在正比例函数y=kx(k≠0)的图象上,则正比例函数的解析式为_____.
相关试题

