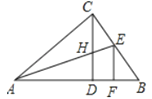
【题目】如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,下列结论:①∠ACD=∠B;②CH=CE=EF;③AC=AF;④CH=HD.其中正确的结论为( )
A.①②④ B.①②③ C. ②③ D.①③
参考答案:
【答案】B
【解析】
试题分析:根据等角的余角相等可判断①;先判断CD∥EF,根据平行线的性质得出∠CEH=∠CHE,再由角平分线的性质可判断②;用AAS判定△ACE≌△AFE,可判断③;根据②,结合图形可判断④.
∵∠B和∠ACD都是∠CAB的余角,∴∠ACD=∠B,故①正确;
∵CD⊥AB,EF⊥AB,∴EF∥CD,∴∠AEF=∠CHE,∴∠CEH=∠CHE,∴CH=CE=EF,故②正确;
∵角平分线AE交CD于H,∴∠CAE=∠BAE,∴△ACE≌△AFE(AAS),∴AC=AF,故③正确;
CH=CE=EF>HD,故④错误.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地市话的收费标准是:(1)通话时间在3分钟以内(含3分钟)话费为0.22元;(2)通话时间超过3分钟时,超过部分按每分钟0.11元计,小王某次的市话费为0.77元,则小王的通话时间为____分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)△ABC的面积为
(2) 画出格点△ABC(顶点均在格点上)关于x轴对称的△

(3)指出△
 的顶点坐标.
的顶点坐标.  ( , ),
( , ),  ( , ),
( , ),  ( , )
( , ) (4)在y轴上画出点Q,使
 最小。
最小。
-
科目: 来源: 题型:
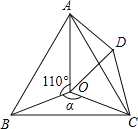
查看答案和解析>>【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)△AOD能否为等边三角形?为什么?
(4)探究:当α为多少度时,△AOD是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a、b是直角三角形的两条直角边,若该三角形的周长为12,斜边长为5,则ab的值是( )
A. 6B. 8C. 12D. 24
-
科目: 来源: 题型:
查看答案和解析>>【题目】爸爸为小明存了一个3年期的教育储蓄(3年期的年利率为2.7%),3年后能取5 405元,他开始存入了____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+kx+3=0的一个根为x=3,则方程的另一个根为 .
相关试题

