【题目】如图,在△ ![]() 中,点
中,点 ![]() ,
, ![]() ,
, ![]() 分别是边
分别是边 ![]() ,
, ![]() ,
, ![]() 的中点,且
的中点,且 ![]() .
.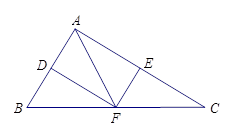
(1)求证:四边形 ![]() 为矩形;
为矩形;
(2)若 ![]() ,
, ![]() ,写出矩形
,写出矩形 ![]() 的周长.
的周长.
参考答案:
【答案】
(1)
证明:连接 ![]() .
.
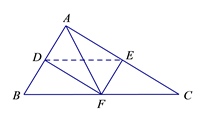
∵ ![]() ,
, ![]() 分别是边
分别是边 ![]() ,
, ![]() 的中点,
的中点,
∴ ![]() ,
, ![]() .
.
∵点 ![]() 是边
是边 ![]() 的中点,
的中点,
∴ ![]() .
.
∴ ![]()
∴四边形 ![]() 为平行四边形.
为平行四边形.
由点 ![]() ,
, ![]() 分别是边
分别是边 ![]() ,
, ![]() 的中点,可得:
的中点,可得:
![]() .
.
∵ ![]() ,
,
∴ ![]() ,即
,即 ![]() .
.
∴四边形 ![]() 为矩形.
为矩形.
(2)
解:由(1)知四边形ADFE为矩形,
∴ △ABC为RT△,且∠BAC=90°.
∵ F为BC中点,AF=2.
∴BC=4
又∵∠C=30° ,
∴AB=2,
∴AC=![]() =2
=2![]() .
.
∴![]()
【解析】(1)连接 D E,由D、 E 、 F 分别是中点,得到EF∥AD ,AD=EF,根据一组对边平行且相等的四边形为平行四边形. 再根据平行四边形的性质即与已知条件得DE=AF .根据对角线相等的平行四边形为矩形.
(2)由(1)知四边形ADFE为矩形,由矩形性质得△ABC为RT△,且∠BAC=90°.根据直角三角形斜边上的中线等于斜边的一半由AF=2得BC=4.再由∠C=30° ,得AB=2,由勾股定理得AC=![]() =2
=2![]() .从而求出四边形ADFE的周长。
.从而求出四边形ADFE的周长。![]()
【考点精析】根据题目的已知条件,利用三角形中位线定理和平行四边形的判定的相关知识可以得到问题的答案,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的周长为13,其中一边长为3,则该等腰三角形的底边长为( )
A. 3 B. 5 C. 7或3 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,正方形
中,正方形  的顶点
的顶点 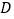 在
在 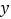 轴上,且
轴上,且 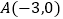 ,
, 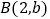 ,则正方形
,则正方形 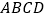 的面积是( )
的面积是( )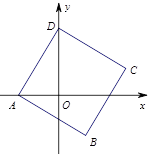
A.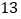
B.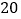
C.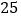
D.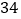
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知点
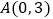 、点
、点 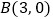 ,一次函数
,一次函数 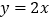 的图象与直线
的图象与直线 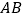 交于点
交于点 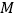 .
.
(1)求直线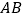 的函数解析式及
的函数解析式及 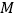 点的坐标;
点的坐标;
(2)若点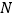 是
是 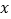 轴上一点,且△
轴上一点,且△ 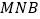 的面积为6,求点
的面积为6,求点  的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,M为线段AB的中点,C点将线段MB分成MC:CB=1:2的两部分,若MC=2,求线段AB的长.

从(1)、(2)中任选一道小题解答.
(1)认真阅读,理解题意,把解题过程补充完整:
解:因为MC:CB=1:2,MC=2.
所以CB=
所以MB=+=6
因为M是AB中点,
所以AB= . MB=
(2)若你有别的计算方法,也可以独立完成. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
2016年人均阅读16本书!
2017年4月23日“世界读书日”之前,国际网络电商亚马逊发布了“亚马逊中国2017全民阅读报告”.报告显示,大部分读者已养成一定的阅读习惯,阅读总量在10本以上的占56%,而去年阅读总量在10本以上的占48%.
京东图书也发布了2016年度图书阅读报告.根据京东图书文娱业务部数据统计,2016年销售纸书人均16册,总量叠在一起相当于15000个帝国大厦的高.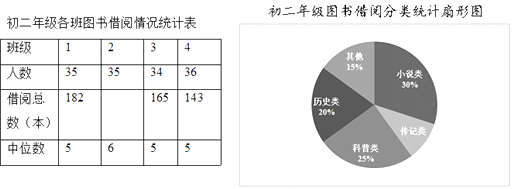
(1)在亚马逊这项调查中,以每年有效问卷1.4万份来计,2017年阅读量十本以上的人数比去年增加了人;
(2)小雨作为学校的图书管理员,根据初二年级每位同学本学期的借书记录,对各个班借阅的情况作出了统计,并绘制统计图表如下:
①全年级140名同学中有科技社团成员40名,他们人均阅读科普类书籍1.5本,年级其他同学人均阅读科普类书籍1.08本,请你计算全年级人均阅读科普类书籍的数量,再通过计算补全统计表;
②在①的条件下,若要推荐初二某个班级为本学期阅读先进集体,你会推荐哪个班,请写出你的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCO中,O为坐标原点,A在y轴上,C在x轴上,B的坐标为(8,6),P是线段BC上动点,点D是直线y=2x﹣6上第一象限的点,若△APD是等腰直角三角形,则点D的坐标为_____________。
相关试题

