【题目】(本题满分8分)如图,四边形ABCD中,![]() ,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.
,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.
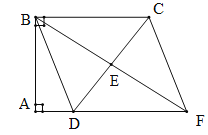
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
参考答案:
【答案】(1)见解析;(2)6![]() 或
或![]()
【解析】
试题(1)根据平行线的性质和中点的性质证明三角形全等,然后根据对角线互相平分的四边形是平行四边形完成证明;
(2)由等腰三角形的性质,分三种情况:①BD=BC,②BD=CD,③BC=CD,分别求四边形的面积.
试题解析:(1)证明:∵∠A=∠ABC=90°
∴AF∥BC
∴∠CBE=∠DFE,∠BCE=∠FDE
∵E是边CD的中点
∴CE=DE
∴△BCE≌△FDE(AAS)
∴BE=EF
∴四边形BDFC是平行四边形
(2)若△BCD是等腰三角形
①若BD=DC
在Rt△ABD中,AB=![]()
∴四边形BDFC的面积为S=![]() ×3=6
×3=6![]() ;
;
②若BD=DC
过D作BC的垂线,则垂足为BC得中点,不可能;
③若BC=DC
过D作DG⊥BC,垂足为G
在Rt△CDG中,DG=![]()
∴四边形BDFC的面积为S=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移或轴对称或旋转对称都可以得到△OBD。
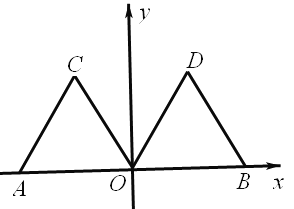
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 个单位长度;△AOC与△OBD关于直线对称,则对称轴是 ;△AOC绕原点O顺时针旋转得到△OBD,则旋转角可以是 度;
(2)连接AD,交OC于点E,求∠AEO的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴是初中数学的一个重要工具.利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b.
如图:
已知数轴上有A、B两点,分别表示的数为﹣10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).
(综合运用).
(1)点A运动2秒后所在位置的点表示的数为 ;点B运动3秒后所在位置的点表示的数为 ;
(2)它们按上述方式运动,A、B两点经过多少秒会相遇,相遇点所表示的数是什么?
(3)它们按上述方式运动,A、B两点经过多少秒后相距2个单位长度?
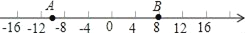
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+4与x轴、y轴分别交于点E,F.将菱形ABCD沿x轴向左平移k个单位,当点C落在△EOF的内部时(不包括三角形的边),k的值可能是( )

A.2 B.3 C.4 D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴是初中数学的一个重要工具.利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b.
如图:
已知数轴上有A、B两点,分别表示的数为﹣10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).
(综合运用).
(1)点A运动2秒后所在位置的点表示的数为 ;点B运动3秒后所在位置的点表示的数为 ;
(2)它们按上述方式运动,A、B两点经过多少秒会相遇,相遇点所表示的数是什么?
(3)它们按上述方式运动,A、B两点经过多少秒后相距2个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】目前,某市正积极推进“五城联创”,其中扩充改造绿地是推进工作计划之一.现有一块直角三角形绿地,量得两直角边长分别为a=9m和b=12m,现要将此绿地扩充改造为等腰三角形,且扩充部分包含以b=12m为直角边的直角三角形,则扩充后等腰三角形的周长为___________.
相关试题

