【题目】阅读理解：

我们把满足某种条件的所有点所组成的图形，叫做符合这个条件的点的轨迹．

例如：角的平分线是到角的两边距离相等的点的轨迹．

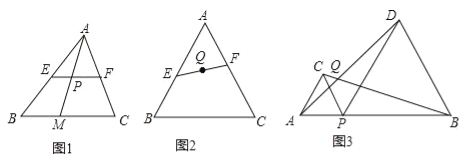
问题：如图1，已知EF为△ABC的中位线，M是边BC上一动点，连接AM交EF于点P，那么动点P为线段AM中点．

理由：∵线段EF为△ABC的中位线，∴EF∥BC，

由平行线分线段成比例得：动点P为线段AM中点．

由此你得到动点P的运动轨迹是： ．

知识应用：

如图2，已知EF为等边△ABC边AB、AC上的动点，连结EF；若AF=BE，且等边△ABC的边长为8，求线段EF中点Q的运动轨迹的长．

拓展提高：

如图3，P为线段AB上一动点（点P不与点A、B重合），在线段AB的同侧分别作等边△APC和等边△PBD，连结AD、BC，交点为Q．

（1）求∠AQB的度数；

（2）若AB=6，求动点Q运动轨迹的长．

参考答案：

【答案】阅读理解：EF；知识应用：4；拓展提高：（1）∠AQB=120°，（2）动点Q运动轨迹的长π．

【解析】

试题分析：阅读理解：根据轨迹的定义可知，动点P的运动轨迹是线段EF．知识应用：如图1中，作△ABC的中位线MN，作EG∥AC交NM的延长线于G，EF与MN交于点Q′，△GQ′E≌△NQ′F，推出Q、Q′重合即可解决问题．拓展提高：如图2中，（1）只要证明△APD≌△CPB，推出∠DQG=∠BPG=60°结论解决问题．（2）由（1）可知点P的运动轨迹是，设弧AB所在圆的圆心为O，Z 圆上任意取一点M，连接AM，BM，则∠M=60°，作OH⊥AB于H，则AH=BH=3，OH=，OB=2，利用弧长公式即可解决．

试题解析：阅读理解：根据轨迹的定义可知，动点P的运动轨迹是线段EF．

知识应用：如图1中，作△ABC的中位线MN，作EG∥AC交NM的延长线于G，EF与MN交于点Q′

∵△ABC是等边三角形，MN是中位线，

∴AM=BM=AN=CN，

∵AF=BE，

∴EM=FN，

∵MN∥BC，

∴∠AMN=∠B=∠GME=60°，

∵∠A=∠GEM=60°，

∴△GEM是等边三角形，

∴EM=EG=FN，

在△GQ′E和△NQ′F中，

，

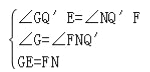∴△GQ′E≌△NQ′F，

∴EQ′=FQ′，

∵EQ=QF，

′点Q、Q′重合，

∴点Q在线段MN上，

∴段EF中点Q的运动轨迹是线段MN，

MN=BC=×8=4．

∴线段EF中点Q的运动轨迹的长为4．

拓展提高：如图2中，

（1）∵△APC，△PBD都是等边三角形，

∴AP=PC，PD=PB，∠APC=∠DPB=60°，

∴∠APD=∠CPB，

在△APD和△CPB中，

，

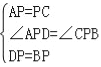∴△APD≌△CPB，

∴∠ADP=∠CBP，设BC与PD交于点G，

∵∠QGD=∠PGB，

∴∠DQG=∠BPG=60°，

∴∠AQB=180°﹣∠DQG=120°

（2）由（1）可知点P的运动轨迹是，设弧AB所在圆的圆心为O，Z 圆上任意取一点M，连接AM，BM，则∠M=60°，

∴∠AOB=2∠M=120°，作OH⊥AB于H，则AH=BH=3，OH=，OB=2，

∴弧AB的长==π．

∴动点Q运动轨迹的长π．

关闭