【题目】我市某中学九年级(1)班开展“阳光体育运动”,决定自筹资金为班级购买体育器材,全班50名同学筹款情况如下表:
筹款金额(元) | 5 | 10 | 15 | 20 | 25 | 30 |
人数 | 3 | 7 | 11 | 11 | 13 | 5 |
则该班同学筹款金额的众数和中位数分别是( )
A.11,20
B.25,11
C.20,25
D.25,20
参考答案:
【答案】D
【解析】解:在这一组数据中25元是出现次数最多的,故众数是25元;
将这组数据已从小到大的顺序排列,处于中间位置的两个数是20、20,那么由中位数的定义可知,这组数据的中位数是20;
故选:D.
中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);众数是一组数据中出现次数最多的数据.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
 与一次函数y=x+2的图象交于点A(﹣3,m).
与一次函数y=x+2的图象交于点A(﹣3,m).(1)求反比例函数的解析式;
(2)如果点M的横、纵坐标都是不大于3的正整数,求点M在反比例函数图象上的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2011个格子中的数为 ( )

A. 3 B. 2 C. 0 D. -1
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
我们把满足某种条件的所有点所组成的图形,叫做符合这个条件的点的轨迹.
例如:角的平分线是到角的两边距离相等的点的轨迹.
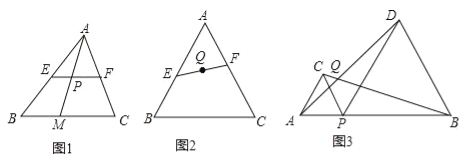
问题:如图1,已知EF为△ABC的中位线,M是边BC上一动点,连接AM交EF于点P,那么动点P为线段AM中点.
理由:∵线段EF为△ABC的中位线,∴EF∥BC,
由平行线分线段成比例得:动点P为线段AM中点.
由此你得到动点P的运动轨迹是: .
知识应用:
如图2,已知EF为等边△ABC边AB、AC上的动点,连结EF;若AF=BE,且等边△ABC的边长为8,求线段EF中点Q的运动轨迹的长.
拓展提高:
如图3,P为线段AB上一动点(点P不与点A、B重合),在线段AB的同侧分别作等边△APC和等边△PBD,连结AD、BC,交点为Q.
(1)求∠AQB的度数;
(2)若AB=6,求动点Q运动轨迹的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某校排球队员的年龄分布:
年龄/岁
13
14
15
16
人数
1
4
5
2
则该校女子排球队员的平均年龄为(结果取整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班10名学生体育测试的成绩(单位:分)分别为:58,60,59,52,58,55,57,58,49,57,则这组数据的众数、中位数分别为( )
A.58,57.5B.57,57.5C.58,58D.58,57
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过第一、二、三象限,则b的值可以是( )
A.﹣2B.﹣1C.0D.2
相关试题

