【题目】如图,A(-4,![]() ),B(-1,2)是一次函数y=kx+b的图像与反比例函数
),B(-1,2)是一次函数y=kx+b的图像与反比例函数![]() (m≠0,m<0)的函数图像的两个交点,AC⊥x轴于点C,BD⊥y轴于点D
(m≠0,m<0)的函数图像的两个交点,AC⊥x轴于点C,BD⊥y轴于点D
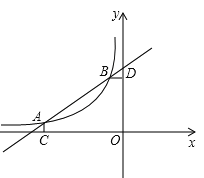
(1)根据函数图像直接回答问题:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?
(2)求一次函数的表达式及m的值;
(3)点P是线段AB上一点,连接PC,PD,若△PCA和△PBD的面积相等,求点P的坐标。
参考答案:
【答案】(1)-4<x<-1;(2)y=![]() ,m=-2;(3)P点坐标是(-
,m=-2;(3)P点坐标是(-![]() ,
,![]() ).
).
【解析】
试题分析:(1)根据一次函数图象在上方的部分是不等式的解,观察图象,可得答案;
(2)根据待定系数法,可得函数解析式;
(3)根据三角形面积相等,可得答案.
试题解析:(1)由图象得一次函数图象在上的部分,-4<x<-1,
当-4<x<-1时,一次函数大于反比例函数的值;
(2)设一次函数的解析式为y=kx+b,
y=kx+b的图象过点(-4,![]() ),(-1,2),则
),(-1,2),则
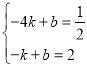 ,解得
,解得![]()
一次函数的解析式为y=![]() ,
,
反比例函数y=![]() 图象过点(-1,2),
图象过点(-1,2),
m=-1×2=-2;
(3)连接PC、PD,如图,
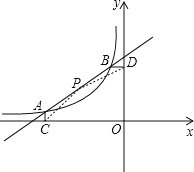
设P(x,![]() x+
x+![]() )
)
由△PCA和△PDB面积相等得
![]() ×
×![]() ×(x+4)=
×(x+4)=![]() ×|-1|×(2-
×|-1|×(2-![]() x-
x-![]() ),
),
x=-![]() ,y=
,y=![]() x+
x+![]() =
=![]() ,
,
∴P点坐标是(-![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
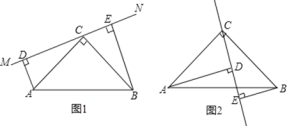
(1)求证:①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,DE、AD、BE又怎样的关系?并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据图(1)所示的程序,得到了y与x的函数图象如图(2),过y轴上一点M作PQ∥x轴交图象于点P,Q,连接OP,OQ.则以下结论:①当x<0时,y=
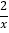 ;②△OPQ的面积为定值;③当x>0时,y的值随x值的增大而增大;④MQ=2PM;⑤∠POQ可以等于90°.其中正确的结论是( )
;②△OPQ的面积为定值;③当x>0时,y的值随x值的增大而增大;④MQ=2PM;⑤∠POQ可以等于90°.其中正确的结论是( )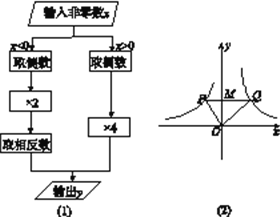
A. ①②④ B. ②④⑤ C. ③④⑤ D. ②③⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,用棋子摆成的“上”字:

第一个“上”字 第二个“上”字 第三个“上”字
如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第四、第五个“上”字分别需用 和 枚棋子.
(2)第n个“上”字需用 枚棋子.
(3)如果某一图形共有102枚棋子,你知道它是第几个“上”字吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点P在线段AB外,且PA=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )

A. 作∠APB的平分线PC交AB于点C
B. 过点P作PC⊥AB于点C且AC=BC
C. 取AB中点C,连接PC
D. 过点P作PC⊥AB,垂足为C
-
科目: 来源: 题型:
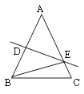
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=32cm,DE是AB的垂直平分线,分别交AB、AC于D、E两点.(1)若∠C=700,则∠CBE=______;(2)若BC=21cm,则△BCE的周长是______cm.
相关试题

