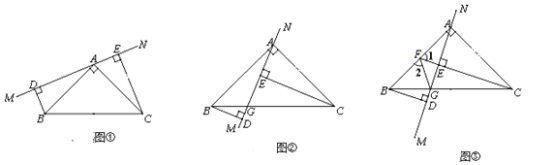
【题目】如图①,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .
. ![]() 是经过点
是经过点![]() 的直线,
的直线, ![]() 于
于![]() ,
, ![]() 于
于![]() .
.
(1)求证: ![]() .
.
(2)若将![]() 绕点
绕点![]() 旋转,使
旋转,使![]() 与
与![]() 相交于点
相交于点![]() (如图②),其他条件不变,
(如图②),其他条件不变,
求证: ![]() .
.
(3)在(2)的情况下,若![]() 的延长线过
的延长线过![]() 的中点
的中点![]() (如图③),连接
(如图③),连接![]() ,
,
求证: ![]() .
.
参考答案:
【答案】答案见解析
【解析】试题分析:(1)首先证明∠DBA=∠EAC,再证明△ADB≌△CEA,然后根据全等三角形的性质可得BD=AE;
(2)首先证明∠BAD=∠ACE,再证明△ABD≌△ACE,根据全等三角形对应边相等可得BD=AE;
(3)首先证明△ACF≌△ABP,然后再证明△BFG≌△BPG,再根据全等三角形对应角相等可得∠BPG=∠BFG,再根据等量代换可得结论∠1=∠2.
试题解析:
(1)∵BD⊥MN,CE⊥MN
∴∠BDA=∠AEC=90°
∴∠DBA+∠DAB=90°
∵∠BAC=90°
∴∠DAB +∠EAC=90°
∴∠DBA=∠EAC
∵AB = AC
∴△ADB≌△CEA(AAS)
∴BD=AE
(2)∵BD⊥MN,CE⊥MN
∴∠BDA=∠AEC=90°
∴∠DBA+∠DAB=90°
∵∠BAC=90°
∴∠DAB +∠EAC=90°
∴∠DBA=∠EAC
∵AB = AC
∴△ADB≌△CEA(AAS)
∴BD=AE
(3)过B作BP//AC交MN于P,如图所示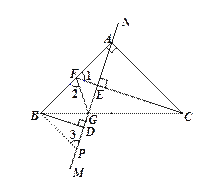
∵BP//AC
∴∠PBA+∠BAC=90°
∵∠BAC=90°
∴∠PBA=∠BAC=90°
由(2)得:△ADB≌△CEA
∴∠BAP=∠ACF
∵AB=AC
∴△ACF≌△ABP(ASA)
∴∠1=∠3
∴AF=BP
∵AB的中点F
∵BF=AF
∴BF=BP
∵∠ABC=45°
又∵∠PBA=90°
∴∠PBG=∠PBA-∠ABC =45°
∴∠ABC=∠PBG
∵BG=BG
∴△BFG≌△BPG(SAS)
∴∠2=∠3
∵∠1=∠3
∴∠1=∠2
-
科目: 来源: 题型:
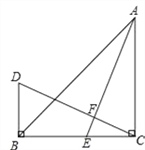
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=BC,BD⊥BC于B,点E在 BC上,CE=BD,DC、AE交于点F.试问DC与AE有何数量与位置关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=2是方程2x﹣5=x+m的解,则m的值是( )
A.1
B.﹣1
C.3
D.﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式m-n的值是1,则代数式3m-3n+2018的值是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某沿海开放城市
 接到台风警报,在该市正南方向
接到台风警报,在该市正南方向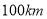 的
的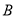 处有一台风中心,沿
处有一台风中心,沿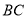 方向以
方向以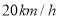 的速度向
的速度向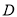 移动,已知城市
移动,已知城市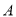 到
到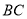 的距离
的距离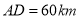 .
.(1)求台风中心经过多长时间从
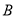 点移到
点移到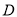 点?
点?(2)如果在距台风中心
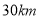 的圆形区域内都将有受到台风的破坏的危险,
的圆形区域内都将有受到台风的破坏的危险,正在
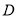 点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?
点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?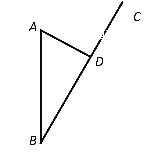
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x-1)2+|y+2|=0,则2x+y=____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,边AB=15,AC=13,高AD=12,则△ABC的周长是
A.42B.32C. 42或32D.不能确定
相关试题

