【题目】已知整数k<5,若△ABC的边长均满足关于x的方程x2﹣3 ![]() x+8=0,则△ABC的周长是 .
x+8=0,则△ABC的周长是 .
参考答案:
【答案】6或12或10
【解析】解:根据题意得k≥0且(3 ![]() )2﹣4×8≥0, 解得k≥
)2﹣4×8≥0, 解得k≥ ![]() ,
,
∵整数k<5,
∴k=4,
∴方程变形为x2﹣6x+8=0,解得x1=2,x2=4,
∵△ABC的边长均满足关于x的方程x2﹣6x+8=0,
∴△ABC的边长为2、2、2或4、4、4或4、4、2.
∴△ABC的周长为6或12或10.
所以答案是:6或12或10.
【考点精析】掌握求根公式和三角形三边关系是解答本题的根本,需要知道根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH=( )

A. cm
cm
B. cm
cm
C. cm
cm
D. cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现用等式AM=(i,j)表示正奇数M是第i组第j个数(从左往右数),如A7=(2,3),则A2013=( )
A.(45,77)
B.(45,39)
C.(32,46)
D.(32,23) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只)
售价(元/只)
甲种节能灯
30
40
甲种节能灯
35
50
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图①,BP、CP分别平分△ABC的外角∠CBD、∠BCE,BQ、CQ分别平分∠PBC、∠PCB,BM、CN分别是∠PBD、∠PCE的角平分线.
(1)当∠BAC=40°时,∠BPC= ,∠BQC= ;
(2)当BM∥CN时,求∠BAC的度数;
(3)如图②,当∠BAC=120°时,BM、CN所在直线交于点O,直接写出∠BOC的度数.
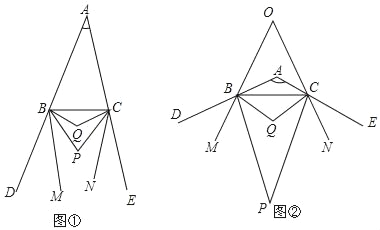
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,给出下列结论: ①2a+b>0;②b>a>c;③若﹣1<m<n<1,则m+n<﹣
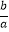 ;④3|a|+|c|<2|b|.
;④3|a|+|c|<2|b|.
其中正确的结论是(写出你认为正确的所有结论序号).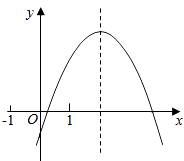
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算: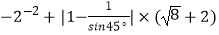 ;
;
(2)解方程: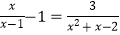 .
.
相关试题

