【题目】二次函数y=ax2+bx+c的图象如图所示,给出下列结论: ①2a+b>0;②b>a>c;③若﹣1<m<n<1,则m+n<﹣ ![]() ;④3|a|+|c|<2|b|.
;④3|a|+|c|<2|b|.
其中正确的结论是(写出你认为正确的所有结论序号).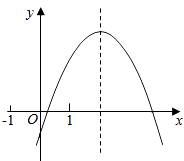
参考答案:
【答案】①③④
【解析】解:∵抛物线开口向下, ∴a<0,
∴2a<0,
对称轴x=﹣ ![]() >1,﹣b<2a,
>1,﹣b<2a,
∴2a+b>0,故选项①正确;
令ax2+bx+c=0,抛物线与轴交于(x1 , 0),(x2 , 0)则x1x2= ![]() ,
,
由图不能准确判断 ![]() 与1大小,则无法确定a,c的大小关系,故选项②不正确
与1大小,则无法确定a,c的大小关系,故选项②不正确
∵﹣1<m<n<1,则﹣2<m+n<2,
∴抛物线对称轴为:x=﹣ ![]() >1,
>1, ![]() >2,m+n
>2,m+n ![]() ,故选项③正确;
,故选项③正确;
当x=1时,a+b+c>0,2a+b>0,3a+2b+c>0,
∴3a+c>﹣2b,∴﹣3a﹣c<2b,
∵a<0,b>0,c<0(图象与y轴交于负半轴),
∴3|a|+|c|=﹣3a﹣c<2b=2|b|,故④选项正确.
所以答案是:①③④.
【考点精析】关于本题考查的二次函数图象以及系数a、b、c的关系,需要了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只)
售价(元/只)
甲种节能灯
30
40
甲种节能灯
35
50
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知整数k<5,若△ABC的边长均满足关于x的方程x2﹣3
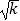 x+8=0,则△ABC的周长是 .
x+8=0,则△ABC的周长是 . -
科目: 来源: 题型:
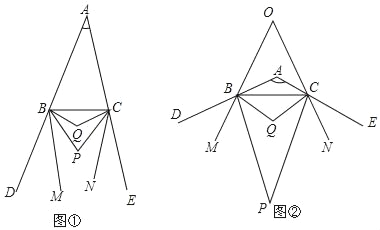
查看答案和解析>>【题目】已知:如图①,BP、CP分别平分△ABC的外角∠CBD、∠BCE,BQ、CQ分别平分∠PBC、∠PCB,BM、CN分别是∠PBD、∠PCE的角平分线.
(1)当∠BAC=40°时,∠BPC= ,∠BQC= ;
(2)当BM∥CN时,求∠BAC的度数;
(3)如图②,当∠BAC=120°时,BM、CN所在直线交于点O,直接写出∠BOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算: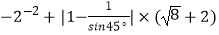 ;
;
(2)解方程: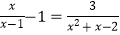 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某批发门市销售两种商品,甲种商品每件售价为300元,乙种商品每件售价为80元.新年来临之际,该门市为促销制定了两种优惠方案:
方案一:买一件甲种商品就赠送一件乙种商品;
方案二:按购买金额打八折付款.
某公司为奖励员工,购买了甲种商品20件,乙种商品x(x≥20)件.
(1)分别写出优惠方案一购买费用y1(元)、优惠方案二购买费用y2(元)与所买乙种商品x(件)之间的函数关系式;
(2)若该公司共需要甲种商品20件,乙种商品40件.设按照方案一的优惠办法购买了m件甲种商品,其余按方案二的优惠办法购买.请你写出总费用w与m之间的关系式;利用w与m之间的关系式说明怎样购买最实惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
相关试题

