【题目】二次函数y=ax2+bx+c(a≠0)的图象经过点A(3,0),B(2,﹣3),并且以x=1为对称轴.
(1)求此函数的解析式;
(2)作出二次函数的大致图象;
(3)在对称轴x=1上是否存在一点P,使△PAB中PA=PB?若存在,求出P点的坐标;若不存在,说明理由.
参考答案:
【答案】(1)解析式为y=x2﹣2x﹣3;(2)画图见解析;(3)存在,点P的坐标为(1,﹣1).
【解析】试题分析:(1)根据对称轴的公式x=![]() 和函数的解析式,将
和函数的解析式,将![]() =1和A(3,0),B(2,﹣3)代入函数解析式,组成方程组解答即可;
=1和A(3,0),B(2,﹣3)代入函数解析式,组成方程组解答即可;
(2)求出图象与坐标轴的交点坐标,描点即可;
(3)根据两点之间距离公式解答即可.
试题解析:解:(1)根据题意得:  ,解得:
,解得: 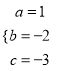 ,∴解析式为y=x2﹣2x﹣3;
,∴解析式为y=x2﹣2x﹣3;
(2)二次函数图象如图:
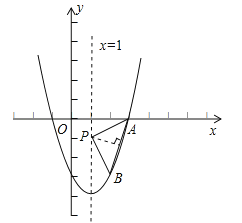
(3)存在.作AB的垂直平分线交对称轴x=1于点P,连接PA、PB,则PA=PB,设P点坐标为(1,m).∵PA=PB,∴22+m2=(﹣3﹣m)2+1,解得:m=﹣1,∴点P的坐标为(1,﹣1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】“今有善行者行一百步,不善行者行六十步”(出自《九章算术》)意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步,假定两者步长相等,据此回答以下问题:
(1)今不善行者先行一百步,善行者追之,不善行者再行六百步,问孰至于前,两者几何步隔之?即:走路慢的人先走100步,走路快的人开始追赶,当走路慢的人再走600步时,请问谁在前面,两人相隔多少步?
(2)今不善行者先行两百步,善行者追之,问几何步及之?即:走路慢的人先走200步,请问走路快的人走多少步才能追上走路慢的人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD(请填空)
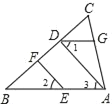
解:∵EF∥AD
∴∠2= (
又∵∠1=∠2
∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=70°( )
∴∠AGD= ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)在Rt△ABC中,∠BAC=
 ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上A,B两点对应的有理数分别为xA=﹣5和xB=6,动点P从点A出发,以每秒1个单位的速度沿数轴在A,B之间往返运动,同时动点Q从点B出发,以每秒2个单位的速度沿数轴在B,A之间往返运动.设运动时间为t秒.
(1)当t=2时,点P对应的有理数xP=______,PQ=______;
(2)当0<t≤11时,若原点O恰好是线段PQ的中点,求t的值;
(3)我们把数轴上的整数对应的点称为“整点”,当P,Q两点第一次在整点处重合时,直接写出此整点对应的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列有理数大小关系判断正确的是( )
A. 0>|﹣10| B. ﹣(﹣
 )>﹣|﹣
)>﹣|﹣ | C. |﹣3|<|+3| D. ﹣1>﹣0.01
| C. |﹣3|<|+3| D. ﹣1>﹣0.01 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△AOB是直角三角形,∠AOB=90°,边AB与y轴交于点C.

(1)若∠A=∠AOC,试说明:∠B=∠BOC;
(2)延长AB交x轴于点E,过O作OD⊥AB,若∠DOB=∠EOB,∠A=∠E,求∠A的度数;
(3)如图,OF平分∠AOM,∠BCO的平分线交FO的延长线于点P,∠A=40°,当△ABO绕O点旋转时(边AB与y轴正半轴始终相交于点C),问∠P的度数是否发生改变?若不变,求其度数;若改变,请说明理由.
相关试题

