【题目】已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,F为BE的中点,连结DF,CF.
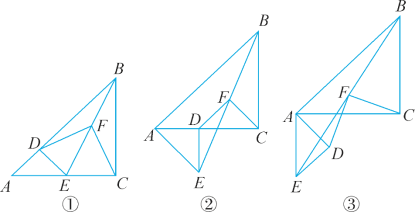
(1)如图①,当点D在AB上,点E在AC上,请直接写出此时线段DF,CF的数量关系和位置关系.
(2)如图②,在(1)的条件下将△ADE绕点A顺时针旋转45°,请你判断此时(1)中的结论是否仍然成立,并证明你的判断.
(3)如图③,在(1)的条件下将△ADE绕点A顺时针旋转90°,若AD=1,AC=![]() ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果).
参考答案:
【答案】(1) DF=CF,DF⊥CF;(2)(1)中的结论仍然成立,证明见解析;(3)CF=![]() .
.
【解析】
(1)根据“直角三角形斜边上的中线等于斜边的一半”可知DF=CF,根据∠DFE=2∠DBF,∠CFE=2∠CBF,得到∠EFD+∠EFC=2∠ABC=90°,DF⊥CF.
(2)延长DF交BC于点G,先证明△DEF≌△GBF,得到DE=GB,DF=GF,根据AD=DE,AB=BC,得到DC=GC又因为∠ACB=90°,所以DF=CF且DF⊥CF.
(3)延长DF交BA于点H,先证明△DEF≌△HBF,得到DE=BH,根据旋转条件可以△ADH为直角三角形,由△ABC和△ADE是等腰直角三角形,AC=2![]() ,可以求出AB的值,进而可以根据勾股定理可以求出DH,再求出DF,求出得CF的值.
,可以求出AB的值,进而可以根据勾股定理可以求出DH,再求出DF,求出得CF的值.
(1) DF=CF. DF⊥CF.
(2)(1)中的结论仍然成立.证明如下:
如解图①,延长DF交BC于点G.
∵∠ADE=∠ACB=90°,∴DE∥BC,
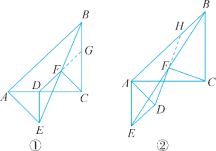
∴∠DEF=∠GBF,∠EDF=∠BGF.
∵F为BE的中点,∴EF=BF,
∴△DEF≌△GBF(AAS),
∴DE=GB,DF=GF.
∵AD=DE,∴AD=GB.
∵AC=BC,∴AC-AD=BC-GB,即DC=GC.
∵∠ACB=90°,∴△DCG是等腰直角三角形.
∵DF=GF,∴DF=CF,DF⊥CF.
(3)CF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
①(2x+1)2=3(2x+1)
②4(x﹣1)2﹣9(3﹣2x)2=0. -
科目: 来源: 题型:
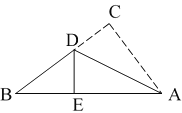
查看答案和解析>>【题目】如图,在三角形纸片 ABC 中,AB=15cm,AC=9cm,BC=12cm, 现将边 AC 沿过点 A 的直线折叠,使它落在 AB 边上.若折痕交 BC 于点 D,点 C 落在点 E 处,你能求出 BD 的长吗?请写出求解过程.
-
科目: 来源: 题型:
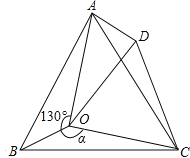
查看答案和解析>>【题目】如图,点O是等边三角形ABC内的一点,∠AOB=130°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.
(1)判断△COD的形状,并加以说明理由.
(2)若AD=1,OC=
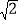 ,OA=
,OA=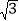 时,求α的度数.
时,求α的度数.(3)探究:当α为多少度时,△AOD是等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=﹣
 +bx+c的图象经过A(2,0)、B(0,﹣6)两点.
+bx+c的图象经过A(2,0)、B(0,﹣6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
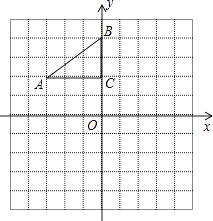
(1)①将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
②若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
(2)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
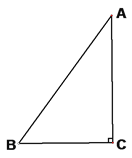
(1)出发2秒后,求△ABP的周长.
(2)问t满足什么条件时,△BCP为直角三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
相关试题

