【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2). 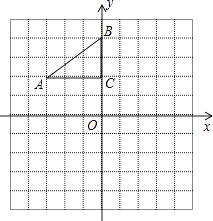
(1)①将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
②若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
(2)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
参考答案:
【答案】
(1)解:①△ABC旋转后对应的△A1B1C,△ABC平移后对应的△A2B2C2如图所示
②如图所示:旋转中心的坐标为:( ![]() ,﹣1)
,﹣1)
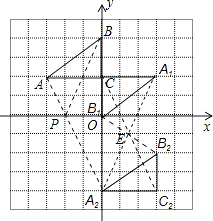
(2)解:∵PO∥AC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴OP=2,
∴点P的坐标为(﹣2,0)
【解析】(1)延长AC到A1 , 使得AC=A1C,延长BC到B1 , 使得BC=B1C,利用点A的对应点A2的坐标为(0,﹣4),得出图象平移单位,即可得出△A2B2C2;根据△△A1B1C绕某一点旋转可以得到△A2B2C2进而得出,旋转中心即可;(2)根据B点关于x轴对称点为A2 , 连接AA2 , 交x轴于点P,再利用相似三角形的性质求出P点坐标即可.
【考点精析】解答此题的关键在于理解轴对称-最短路线问题的相关知识,掌握已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.
-
科目: 来源: 题型:
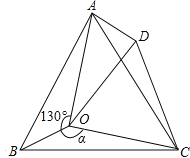
查看答案和解析>>【题目】如图,点O是等边三角形ABC内的一点,∠AOB=130°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.
(1)判断△COD的形状,并加以说明理由.
(2)若AD=1,OC=
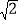 ,OA=
,OA=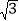 时,求α的度数.
时,求α的度数.(3)探究:当α为多少度时,△AOD是等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,F为BE的中点,连结DF,CF.
(1)如图①,当点D在AB上,点E在AC上,请直接写出此时线段DF,CF的数量关系和位置关系.
(2)如图②,在(1)的条件下将△ADE绕点A顺时针旋转45°,请你判断此时(1)中的结论是否仍然成立,并证明你的判断.
(3)如图③,在(1)的条件下将△ADE绕点A顺时针旋转90°,若AD=1,AC=
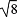 ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=﹣
 +bx+c的图象经过A(2,0)、B(0,﹣6)两点.
+bx+c的图象经过A(2,0)、B(0,﹣6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
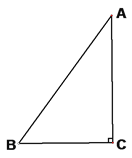
(1)出发2秒后,求△ABP的周长.
(2)问t满足什么条件时,△BCP为直角三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②﹣b<a+c;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论有( )
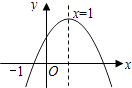
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)x2﹣4x+1=0
(2)3(x﹣2)2=x(x﹣2).
相关试题

