【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(2,0),抛物线的对称轴x=-1与抛物线交于点D,与直线BC交于点E.

(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形BOCF的面积最大,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
参考答案:
【答案】(1)抛物线的解析式为y=-![]() x2-x+4;(2)存在,F(-2,4); (3)点P的坐标(-3,1).
x2-x+4;(2)存在,F(-2,4); (3)点P的坐标(-3,1).
【解析】试题分析: (1)根据函数值相等的两点关于对称轴对称,可得B点坐标,根据待定系数法,可得函数解析式;
(2)根据面积的和差,可得二次函数,根据二次函数的性质,可得m的值,再根据自变量与函数值的对应关系,可得F点坐标;
(3)根据平行四边形的对边相等,可得关于m的方程,根据解方程,可得答案.
试题解析:
(1)由A、B关于对称轴对称,A点坐标为(2,0),得 B(-4,0).
将A、B、C点的坐标代入函数解析式,得 ,
,
解得 ,
,
抛物线的解析式为y=-![]() x2-x+4;
x2-x+4;
(2)如图1,
 ,
,
设BC的解析式为y=kx+b,
将B、C点坐标代入函数解析式,得![]() ,
,
解得![]() ,
,
BC的解析式为y=x+4.
G在BC上,D在抛物线上,得
G(m,m+4),F(m,-![]() m2-m+4).
m2-m+4).
DG=-![]() m2-m+4-(m+4)=-
m2-m+4-(m+4)=-![]() m2-2m.
m2-2m.
S四边形BOCF=S△BOC+S△BCF=![]() BOOC+
BOOC+![]() FGBO
FGBO
=![]() ×4×4+
×4×4+![]() ×4(-
×4(-![]() m2-2m)
m2-2m)
=8+2[-![]() (m+2)2+2]
(m+2)2+2]
当m=-2时,四边形BOCF的面积最大是12,
当m=-2时,-![]() m2-m+4=4,即F(-2,4);
m2-m+4=4,即F(-2,4);
(3)如图2
 ,
,
当x=-1时,y=-![]() x2-x+4=
x2-x+4=![]() ,即D(-1,
,即D(-1, ![]() )
)
y=x+4=3,即E(-1,3).
DE=![]() -3=
-3=![]() .
.
P在直线BC上,Q在抛物线上,得
P(m,m+4),Q(m,-![]() m2-m+4).
m2-m+4).
PQ=-![]() m2-m+4-(m+4)=-
m2-m+4-(m+4)=-![]() m2-2m.
m2-2m.
由以D、E、P、Q为顶点的四边形是平行四边形,得
DE=PQ,即-![]() m2-2m=
m2-2m=![]() ,
,
解得m=-1(不符合题意,舍),m=-3.
当m=-3时,y=m+4=1,
即P(-3,1).
以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标(-3,1).
点睛: 本题考查了二次函数综合题,利用函数值相等的两点关于对称轴对称得出B点坐标是解题关键;利用面积的和差得出二次函数是解题关键;利用平行四边形的对边相等得出关于m的方程是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,⊙C与y轴相切于D点,与x轴相交于A(2,0)、B(8,0)两点,圆心C在第四象限.
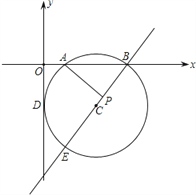
(1)求点C的坐标;
(2)连接BC并延长交⊙C于另一点E,若线段BE上有一点P,使得AB2=BPBE,能否推出AP⊥BE?请给出你的结论,并说明理由;
(3)在直线BE上是否存在点Q,使得AQ2=BQEQ?若存在,求出点Q的坐标;若不存在,也请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD.
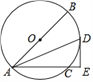
(1)求证:DE是⊙O的切线;
(2)若
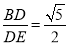 ,AD=4
,AD=4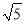 ,求CE的长.
,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋中有4个红球、5个白球、11个黄球,它们除颜色外都相同.
(1)求从袋中摸出一个球是红球的概率;
(2)现从袋中取走若干个黄球,并放入相同数量的红球,搅拌均匀后,要使从袋中摸出一个球是红球的概率不小于
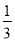 ,问至少需取走多少个黄球?
,问至少需取走多少个黄球? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两圆相离,半径分别为2cm、3cm,则两圆圆心距d范围为_____.
-
科目: 来源: 题型:
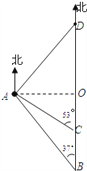
查看答案和解析>>【题目】如图,一艘货船以每小时48海里的速度从港口B出发,沿正北方向航行.在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处,测得A处在C处的北偏西53°方向上,且A、C之间的距离是45海里.在货船航行的过程中,求货船与灯塔A之间的最短距离及B、C之间的距离;若货船从港口B出发2小时后到达D,求A、D之间的距离.
(参考数据:sin53°≈
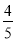 ,cos53°≈
,cos53°≈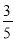 ,tan53°≈
,tan53°≈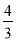 )
) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.x2+x2=x4
B.x2+x3=2x5
C.3x﹣2x=1
D.x2y﹣2x2y=﹣x2y
相关试题

