【题目】如图,在△ABC中,BA=BC=20cm,AC=30cm,点P从A出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以3cm/s的速度向A点运动.设运动时间为x(s).
(1)当x为何值时,PQ∥BC;
(2)当△APQ与△CQB相似时,AP的长为 . ;
(3)当S△BCQ:S△ABC=1:3,求S△APQ:S△ABQ的值.
参考答案:
【答案】
(1)
解:由题意得,PQ平行于BC,则AP:AB=AQ:AC,AP=4x,AQ=30﹣3x
∴ ![]() =
= ![]()
∴x= ![]() ;
;
(2)![]()
cm或20cm
(3)
解:当S△BCQ:S△ABC=1:3时, ![]() =
= ![]() ,
,
∴ ![]() ,
,
由(1)知,PQ∥BC,
∴△APQ∽△ABC,
∴ ![]() ,
,
∴S△APQ:S△ABQ=2.
【解析】解: (2)假设两三角形可以相似,
情况1:当△APQ∽△CQB时,CQ:AP=BC:AQ,
即有 ![]() =
= ![]() 解得x=
解得x= ![]() ,
,
经检验,x= ![]() 是原分式方程的解.
是原分式方程的解.
此时AP= ![]() cm,
cm,
情况2:当△APQ∽△CBQ时,CQ:AQ=BC:AP,
即有 ![]() =
= ![]() 解得x=5,
解得x=5,
经检验,x=5是原分式方程的解.
此时AP=20cm.
综上所述,AP= ![]() cm或AP=20cm;
cm或AP=20cm;
故答案为: ![]() cm或20cm;
cm或20cm;
(1)当PQ∥BC时,根据平行线分线段成比例定理,可得出关于AP,PQ,AB,AC的比例关系式,我们可根据P,Q的速度,用时间x表示出AP,AQ,然后根据得出的关系式求出x的值.(2)本题要分两种情况进行讨论.已知了∠A和∠C对应相等,那么就要分成AP和CQ对应成比例以及AP和BC对应成比例两种情况来求x的值;(3)当S△BCQ:S△ABC=1:3时, ![]() =
= ![]() ,于是得到
,于是得到 ![]() ,通过相似三角形的性质得到
,通过相似三角形的性质得到 ![]() ,即可得到结论.
,即可得到结论.
-
科目: 来源: 题型:
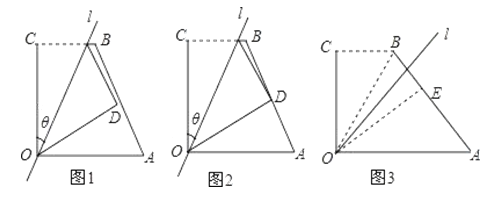
查看答案和解析>>【题目】(阅读)如图1,四边形OABC中,OA=a,OC=3,BC=2,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ [θ,a ]
(理解)若点D与点A重合,则这个操作过程为FZ [45°,3];
(尝试)
(1)若点D恰为AB的中点(如图2),求θ;
(2)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形OABC的边AB上(如图3),求出a的值;若点E落在四边形OABC的外部,直接写出a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个构造完全相同(除所标数字外)的转盘A、B,游戏规定:转动两个转盘各一次,指向大的数字获胜.
(1)用树状图或列表格列出两个转盘转出的所有可能出现的结果;
(2)如果由你和小明各选择一个转盘游戏,你会选择哪一个,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y=
 与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4).
与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4).
(1)试确定这两函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并求△AOB的面积;
(3)根据图象直接写出反比例函数值大于一次函数值的x的取值范围. -
科目: 来源: 题型:
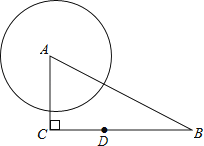
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
A.1<r<4
B.2<r<4
C.1<r<8
D.2<r<8 -
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了正方形之后,给同桌小文出了错题,从下列四个条件:
①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图所示),现有如下四种选法,你认为其中错误的是( )
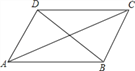
A. ①② B. ①③ C. ②③ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|
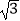 ﹣1|﹣
﹣1|﹣ 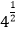 ﹣
﹣ 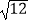 +
+ 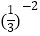 .
.
相关试题

