搜索
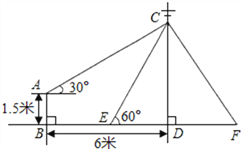
【题目】如图，在电线杆上的C处引拉线CE、CF固定电线杆，拉线CE和地面所成的角
∠CED=60°，在离电线杆6米的B处安置测角仪AB，在A处测得电线杆上C处的仰角为30°，已知测角仪高AB为1.5米，求拉线CE的长 （结果精确到0.1米，参考数据：
≈1.414，
≈1.732）．
参考答案：
【答案】5.7米
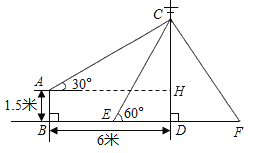
【解析】试题分析：过点A作AH⊥CD，垂足为H．在Rt△ACH中求出CH．在Rt△ECD中，再求出EC即可．
试题解析：解：过点A作AH⊥CD，垂足为H．由题意可知四边形ABDH为矩形，∠CAH=30°，∴AB=DH=1.5，BD=AH=6．在Rt△ACH中，tan∠CAH=
，∴CH=AHtan∠CAH，∴CH=AHtan∠CAH=6tan30°=6×
=2
．∵DH=1.5，∴CD=2+1.5．在Rt△CDE中，∵∠CED=60°，sin∠CED=
，∴CE=
=4+≈5.7（米）．
答：拉线CE的长约为5.7米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中，AC=BC，∠ACB=90°，直角∠DFE的顶点F是AB中点，两边FD，FE分别交AC，BC于点D，E两点，当∠DFE在△ABC内绕顶点F旋转时（点D不与A，C重合），给出以下个结论：①CD=BE；②四边形CDFE不可能是正方形；③△DFE是等腰直角三角形；④S四边形CDFE=
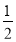S△ABC．上述结论中始终正确的有______．（填序号）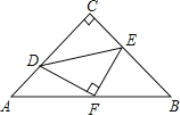
-
科目： 来源： 题型：
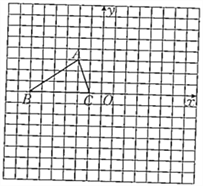
查看答案和解析>>【题目】如图，已知△ABC的三个顶点的坐标分别为A(-2，3)、B(-6，0)、C(-1，0).
(1)画出将△ABC绕坐标原点O逆时针旋转90°图形.
(2)填空：以A、B、C为顶点的平行四边形的第四个顶点D的坐标为________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在公路 MN 两侧分别有 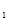A
, A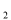
......A
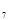,七个工厂,各工厂与公路 MN(图中粗线)之间有小公路连接.现在需要在公路 MN 上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是（ ）.①车站的位置设在 C 点好于 B 点;
②车站的位置设在 B 点与 C 点之问公路上任何一点效果一样;
③车站位置的设置与各段小公路的长度无关.
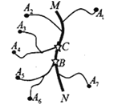
A.①B.②C.①③D.②③
-
科目： 来源： 题型：
查看答案和解析>>【题目】直接填答案：
①（－5）＋（－5）＝______；②（－5）＋（＋8）＝______；③90
（－3）＝______；④（－5）－（－3）＝______；⑤－16－8＝_____；⑥8－16＝______；
⑦
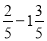＝______；⑧
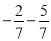＝_____。⑨
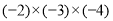＝_____；⑩
＝______。 -
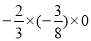科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC 中，D 是 BC 边的中点，E、F 分别在 AD 及其延长线上，CE∥BF，连接BE、CF．
（1）求证：△BDF ≌△CDE；
（2）若 DE =
BC，试判断四边形 BFCE 是怎样的四边形，并证明你的结论．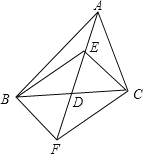
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，E、F是对角线BD上两点，且∠EAF=45°，将△ADF绕点A顺时针旋转90°后，得到△ABQ，连接EQ，求证：
（1）EA是∠QED的平分线；
（2）EF2=BE2+DF2．
相关试题
