【题目】关于二次函数y=ax2+bx+c图象有下列命题:
(1)当c=0时,函数的图象经过原点;
(2)当c>0时,函数的图象开口向下时,方程ax2+bx+c=0必有两个不等实根;
(3)当b=0时,函数图象关于原点对称.
其中正确的个数有( )
A. 0个 B. 1个 C. 2个 D. 3个
参考答案:
【答案】C
【解析】根据二次函数的性质可知:
当c=0时,函数的图象经过原点,正确;
当c>0时,函数的图象开口向下时,图象与轴有个交点,所以方程必有两个不等实根,正确;
当b=0时,函数图象关于轴对称,错误.有两个正确.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组线段长为边,能组成三角形的是( )
A.1cm,2cm,4cm
B.8cm,6cm,4cm
C.12cm,5cm,6cm
D.2cm,3cm,6cm -
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣1,﹣2,0,2这四个数中,最小的一个数是( )
A. ﹣1 B. ﹣2 C. 0 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】对称轴平行于y轴的抛物线的顶点为点(2,3)且抛物线经过点(3,1),那么抛物线解析式是( )
A. y=﹣2x2+8x+3 B. y=﹣2x2﹣8x+3 C. y=﹣2x2+8x﹣5 D. y=﹣2x2﹣8x+2
-
科目: 来源: 题型:
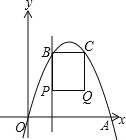
查看答案和解析>>【题目】如图,在平面直角坐标系中,经过原点的抛物线y=-x2+4mx(m>0)与x轴的另一个交点为点A,过点P(1,m)作直线PB⊥x轴,交抛物线于点B,作点B关于抛物线对称轴的对称点C(点B、C不重合),连结BC,当点P、B不重合时,以BP、BC为边作矩形PBCQ,设矩形PBCQ的周长为l.
(1)当m=1时,求点A的坐标.
(2)当BC=
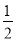 时,求这条抛物线所对应的函数表达式.
时,求这条抛物线所对应的函数表达式.(3)当点P在点B下方时,求l与m之间的函数关系.
(4)连结CP,以CP为直角边作等腰直角三角形PCM,直接写出点M落在坐标轴上时m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一边长等于4,一边长等于9,则它的周长等于( )
A.17
B.22
C.17或22
D.13 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算结果正确的是( )
A. x2+2x2=3x4 B. (﹣2x2)3=8x6 C. x2(﹣x3)=﹣x5 D. 2x2÷x2=x
相关试题

