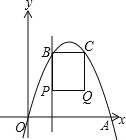
【题目】如图,在平面直角坐标系中,经过原点的抛物线y=-x2+4mx(m>0)与x轴的另一个交点为点A,过点P(1,m)作直线PB⊥x轴,交抛物线于点B,作点B关于抛物线对称轴的对称点C(点B、C不重合),连结BC,当点P、B不重合时,以BP、BC为边作矩形PBCQ,设矩形PBCQ的周长为l.
(1)当m=1时,求点A的坐标.
(2)当BC=![]() 时,求这条抛物线所对应的函数表达式.
时,求这条抛物线所对应的函数表达式.
(3)当点P在点B下方时,求l与m之间的函数关系.
(4)连结CP,以CP为直角边作等腰直角三角形PCM,直接写出点M落在坐标轴上时m的值.
参考答案:
【答案】(1) (4,0);(2) y=-x2+![]() x或y=-x2+
x或y=-x2+![]() x.(3)l=-2m+2.(4)m=
x.(3)l=-2m+2.(4)m=![]() ,m=
,m=![]() .
.
【解析】
试题分析:(1)根据自变量与函数值的对应关系,可得答案;
(2)根据BC的长,可得关于m的方程,根据解方程,可得m的值;
(3)根据周长公式,可得答案;
(4)利用直线PC的斜率求出直线PE的斜率,并求出直线PE的参数方程,讨论点E在x轴与y轴的情况,并分别求出点E的参数坐标,根据PC=PE,利用两点间距离公式求解.此题也可用开锁法进行求解.
试题解析:(1)当m=1时,抛物线的解析式为y=-x2+4x.
当y=0时,-x2+4x=0,解得x1=0,x2=4,即A点坐标为(4,0);
(2)当y=-x2+4mx中x=1时,y=4m-1,B(1,4m-1).且抛物线的对称轴为x=-![]() =2m.
=2m.
当点B在对称轴左侧时,即m>![]() 时,BC=2(2m-1)=4m-2.
时,BC=2(2m-1)=4m-2.
当BC=![]() 时,4m-2=
时,4m-2=![]() .m=
.m=![]() ,这条抛物线的解析式为y=-x2+
,这条抛物线的解析式为y=-x2+![]() x.
x.
当BC=![]() 时,2-4m=
时,2-4m=![]() .m=
.m=![]() ,这条抛物线的解析式为y=-x2+
,这条抛物线的解析式为y=-x2+![]() x.
x.
(3)当点B在对称轴左侧,同时点P在点B的下方,即![]() <m<
<m<![]() 时,
时,
l=2[2(1-2m)+(4m-1-m)],l=-2m+2.
(4)分三种情况:P在对称轴左侧,P(1,m),B(1,4m-1),C(4m-1,4m-1),
BC=4m-2,BP=3m-1,
①若∠CPQ=90°,PC=PQ,如图1,

此时,△CBP≌△PFQ,
∴CB=PF,即4m-2=m,解得m=![]() ,
,
②若∠PCQ=90°,CP=CQ,如图2,

此时,△QFP≌△CDQ,
∴DF=CD,即4m-1=4m-1,方程无解;
∴此种情况不成立.
③如图3,

B(1,4m-1),P(1,m),C(4m-1,4m-1),
若∠CPQ=90°,PC=PQ,△CBP≌△QFC,
BP=CF,即3m-1=4m-1,解得m=0(舍),
④如图4,

∠CQP=90°,CQ=CP,
△CBP≌△PFQ,
BP=QF,即4m-1-m=1,解得m=![]() ;
;
⑤如图5,

∠CQP=90°,CQ=CP,
△CBP≌△PFQ,
BC=PF,即2-4m=m,解得m=![]() ;
;
综上所述:m=![]() ,m=
,m=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣1,﹣2,0,2这四个数中,最小的一个数是( )
A. ﹣1 B. ﹣2 C. 0 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】对称轴平行于y轴的抛物线的顶点为点(2,3)且抛物线经过点(3,1),那么抛物线解析式是( )
A. y=﹣2x2+8x+3 B. y=﹣2x2﹣8x+3 C. y=﹣2x2+8x﹣5 D. y=﹣2x2﹣8x+2
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于二次函数y=ax2+bx+c图象有下列命题:
(1)当c=0时,函数的图象经过原点;
(2)当c>0时,函数的图象开口向下时,方程ax2+bx+c=0必有两个不等实根;
(3)当b=0时,函数图象关于原点对称.
其中正确的个数有( )
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一边长等于4,一边长等于9,则它的周长等于( )
A.17
B.22
C.17或22
D.13 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算结果正确的是( )
A. x2+2x2=3x4 B. (﹣2x2)3=8x6 C. x2(﹣x3)=﹣x5 D. 2x2÷x2=x
-
科目: 来源: 题型:
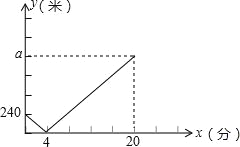
查看答案和解析>>【题目】小明家、学校与图书馆依次在一条直线上,小明、小亮两人同时分别从小明家和学校出发沿直线匀速步行到图书馆借阅图书,小明到达图书馆花了20分钟,小亮每分钟步行40米,小明离学校的距离y(米)与两人出发时间x(分)之间的函数图象如图所示.
(1)小明每分钟步行 米,a= ,小明家离图书馆的距离为 米.
(2)在图中画出小亮离学校的距离y(米)与x(分)之间的函数图象.
(3)求小明和小亮在途中相遇时二人离图书馆的距离.
相关试题

