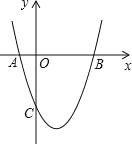
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
参考答案:
【答案】(1)y=x2﹣2x﹣3.(2)对称轴x=1,顶点坐标(1,﹣4).(3)点P在该抛物线上滑动到(1+2![]() ,4)或(1﹣2
,4)或(1﹣2![]() ,4)或(1,﹣4)时,满足S△PAB=8.
,4)或(1,﹣4)时,满足S△PAB=8.
【解析】
试题分析:(1)由于抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,那么可以得到方程x2+bx+c=0的两根为x=﹣1或x=3,然后利用根与系数即可确定b、c的值.
(2)根据S△PAB=8,求得P的纵坐标,把纵坐标代入抛物线的解析式即可求得P点的坐标.
试题解析:(1)∵抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,
∴方程x2+bx+c=0的两根为x=﹣1或x=3,
∴﹣1+3=﹣b,
﹣1×3=c,
∴b=﹣2,c=﹣3,
∴二次函数解析式是y=x2﹣2x﹣3.
(2)∵y=﹣x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的对称轴x=1,顶点坐标(1,﹣4).
(3)设P的纵坐标为|yP|,
∵S△PAB=8,
∴![]() AB|yP|=8,
AB|yP|=8,
∵AB=3+1=4,
∴|yP|=4,
∴yP=±4,
把yP=4代入解析式得,4=x2﹣2x﹣3,
解得,x=1±2![]() ,
,
把yP=﹣4代入解析式得,﹣4=x2﹣2x﹣3,
解得,x=1,
∴点P在该抛物线上滑动到(1+2![]() ,4)或(1﹣2
,4)或(1﹣2![]() ,4)或(1,﹣4)时,满足S△PAB=8.
,4)或(1,﹣4)时,满足S△PAB=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一道题“求多项式a2b3﹣
 ab+b2﹣(4a2b3﹣
ab+b2﹣(4a2b3﹣  ab﹣b2)+(3a2b3+
ab﹣b2)+(3a2b3+  ab)﹣5的值,其中a=2,b=﹣3”.马小虎做题时把a=2错抄成a=﹣2,但他做出的结果却是正确的,你知道这是怎么回事吗?请说明理由,并求出结果.
ab)﹣5的值,其中a=2,b=﹣3”.马小虎做题时把a=2错抄成a=﹣2,但他做出的结果却是正确的,你知道这是怎么回事吗?请说明理由,并求出结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )

A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋中装有大小相同的2个红球和2个绿球.
(1)先从袋中摸出1个球后放回,混合均匀后再摸出1个球.
①求第一次摸到绿球,第二次摸到红球的概率;
②求两次摸到的球中有1个绿球和1个红球的概率;
(2)先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是多少?请直接写出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】芝麻作为食品和药物,均广泛使用.经测算,一粒芝麻约有0.00000201千克,用科学记数法表示为( )
A.2.01×10﹣6千克
B.0.201×10﹣5千克
C.20.1×10﹣7千克
D.2.01×10﹣7千克 -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式
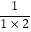 =1﹣
=1﹣  ,
, 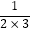 =
=  ﹣
﹣  ,
, 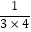 =
=  ﹣
﹣  ,将以上三个等式两边分别相加得:
,将以上三个等式两边分别相加得: 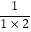 +
+ 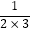 +
+ 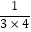 =1﹣
=1﹣  +
+  ﹣
﹣  +
+  ﹣
﹣  =1﹣
=1﹣  =
=  .
.
(1)猜想并写出: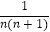 =
=
(2)直接写出下列各式的计算结果: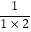 +
+ 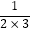 +
+ 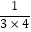 +…+
+…+ 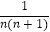 =
=
(3)探究并计算: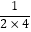 +
+ 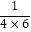 +
+ 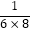 +…+
+…+ 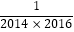 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣7.3)﹣(﹣25.7)+(﹣13.7)﹣(﹣7.3)
(2)( +
+  ﹣
﹣  )÷(﹣
)÷(﹣  )
)
(3)﹣32﹣|﹣6|﹣3×(﹣ )+(﹣2)2÷
)+(﹣2)2÷  .
.
相关试题

