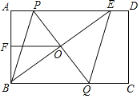
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD,BE,BC于点P,O,Q,连接BP,EQ.
(1)求证:四边形BPEQ是菱形;
(2)F为AB的中点,则线段OF与线段AE有什么位置关系和数量关系,并说明理由;
(3)在(2)的条件下,若AB=6,OF=4,求PQ的长.
参考答案:
【答案】(1)见解析;(2)见解析;(3)PQ=![]() .
.
【解析】
(1)先根据线段垂直平分线的性质证明QB=QE,由ASA证明△BOQ≌△EOP,得出PE=QB,证出四边形BPEQ是平行四边形,再根据菱形的判定即可得出结论;
(2)根据中位线定理即可求出线段OF与线段AE的位置关系和数量关系.
(3)根据勾股定理求出OB的长度,进而求出BE, 设菱形的边长为x,则AP=8﹣x.
在Rt△APB中,根据勾股定理列出方程,求出边长,根据菱形的面积公式进行求解即可.
(1)证明:∵PQ垂直平分BE,
∴PB=PE,OB=OE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,∠PEO=∠QBO,OB=OE,∠POE=∠QOB,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵QB=QE,
∴四边形BPEQ是菱形;
(2)∵四边形BPEQ是菱形,
∴OB=OE.
又∵F是AB的中点,
∴OF是△BAE的中位线,
∴AE∥OF且OF=![]() AE.
AE.
(3)∵AB=6,F是AB的中点,
∴BF=3.
∵OF∥AE,
∴∠BFO=90°.
在Rt△FOB中, ![]()
∴BE=10.
设菱形的边长为x,则AP=8﹣x.
在Rt△APB中,BP2=AB2+AP2,即x2=62+(8﹣x)2,解得:x=![]() .
.
由菱形的面积公式可知: ![]() 解得:PQ
解得:PQ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为A,B,C,D四等级,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题(说明:测试成绩在总人数的前30%考生为A等级,前30%至前70%为B等级,前70%至前90%为C等级,90%以后为D等级)

(1)抽取了 名学生成绩;
(2)请把频数分布直方图补充完整;
(3)扇形统计图中A等级所在的扇形的圆心角度数是 ;
(4)若测试成绩在总人数的前90%为合格,该校初二年级有800名学生,求全年级生物合格的学生共约多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的边AB长为4cm,DE平分∠ADC,若∠B=80°,∠DAE=50°,求平行四边形ABCD的周长?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各句判定矩形的说法
 对角线相等的四边形是矩形;
对角线相等的四边形是矩形; 对角线互相平分且相等的四边形是矩形;
对角线互相平分且相等的四边形是矩形; 有一个角是直角的四边形是矩形;
有一个角是直角的四边形是矩形; 有四个角是直角的四边形是矩形;
有四个角是直角的四边形是矩形; 四个角都相等的四边形是矩形;
四个角都相等的四边形是矩形; 对角线相等,且有一个角是直角的四边形是矩形;是正确有几个
对角线相等,且有一个角是直角的四边形是矩形;是正确有几个
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】通常情况下,
 不一定等于
不一定等于 ,但我们数学上存在这样一些特殊的数对,观察:
,但我们数学上存在这样一些特殊的数对,观察: ,
, ,
, ,…,我们把符合
,…,我们把符合 的两个数叫做“和积数对”,已知
的两个数叫做“和积数对”,已知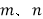
 是一对“和积数对”.
是一对“和积数对”.(1)请举出一对
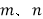 是“和积数对”,并验证其正确性;
是“和积数对”,并验证其正确性;(2)求代数式
 的值;
的值;(3)小明发现了一个关于
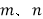 的结论:
的结论: ;你认为小明发现的结论正确吗?请说明理由.
;你认为小明发现的结论正确吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, 分别平分
分别平分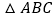 的外角
的外角 、内角
、内角 、外角
、外角 .以下结论:①
.以下结论:① ;②
;② ;③
;③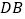 平分
平分 ;④
;④ ;⑤
;⑤ .其中正确的结论有( ).
.其中正确的结论有( ).
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校标准化建设需购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑和每台电子白板各多少万元;
(2)根据学校需要,实际购进电脑和电子白板共30台,总费用30万元,请你通过计算求学校购买了电脑和电子白板各多少台.
相关试题

