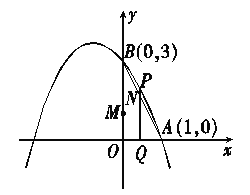
【题目】如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(1)求抛物线对应的函数关系式;
(2)动点Q从点O出发,以每秒1个单位长度的速度在线段OA上运动,同时动点M从O点出发以每秒3个单位长度的速度在线段OB上运动.过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒
①当t为何值时,四边形OMPQ为矩形;
②△AON能否为等腰三角形?若能,求出t的值;若不能,请说明理由.
参考答案:
【答案】(1)y=-![]() -2x+3;(2)①t=
-2x+3;(2)①t=![]() ;②t=
;②t=![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.
【解析】试题分析:(1)将抛物线解析式设成顶点式,然后将(1,0)和(0,3)代入求出函数解析式;(2)将x=t代入二次函数解析式,从而得出PQ的长度,然后根据PQ=OM得出方程,求出t的值;(3)首先求出直线AB的解析式,从而得出点N的坐标,求出ON的长度,然后根据等腰三角形的性质分OA=ON,ON=AN,AN=AO三种情况分别求出t的值.
试题解析:(1)设抛物线的解析式为y=a(x+1)2+k,
将(1,0),(0,3)代入,得![]() ,解得a=-1,k=4,所以抛物线的解析式为y=-x2-2x+3;
,解得a=-1,k=4,所以抛物线的解析式为y=-x2-2x+3;
(2)①将x=t,代入y=-x2-2x+3得y=-t2-2t+3,即PQ=-t2-2t+3,当PQ=OM时四边形OMPQ为矩形,即3t=-t2-2t+3,解得t1=![]() ,t2=
,t2=![]() (舍去),所以当t=
(舍去),所以当t=![]() 时,四边形OMPQ为矩形-
时,四边形OMPQ为矩形-
②△AON能为等腰三角形
理由如下:
设直线AB的解析式为y=kx+b,将(1,0)(0,3)代入,得![]() ,解得k=-3,b=3,
,解得k=-3,b=3,
所以AB的解析式为y=-3x+3,将x=t代入,得y=-3t+3,N点的坐标为(t,-3t+3),
ON=![]()
(Ⅰ)当OA=ON时,△AON是等腰三角形,即1=![]() ,解得t1=1(舍去),t2=
,解得t1=1(舍去),t2=![]() .
.
(Ⅱ)当ON=AN时,△AON是等腰三角形,因为NQ⊥x轴,所以当OQ=QA,即当t=![]() 时,△AON是等腰三角形
时,△AON是等腰三角形
(Ⅲ)当AN=AO时,AN2=NQ2+AQ2=(-3t+3)2+(1-t)2,
即(-3t+3)2+(1-t)2=1,解得t1=![]() ,t2=
,t2=![]() >1,舍去.
>1,舍去.
综上,当t为![]() 秒,
秒,![]() 秒,
秒,![]() 秒时,△AON是等腰三角形.
秒时,△AON是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,2016年某市的初中毕业生人数约有43900人,这个数字用科学记数法可以表示为( )
A.4.39×105
B.43.9×103
C.4.39×104
D.0.439×105 -
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=(x﹣1)2+4先向右平移4个单位长度,再向下平移3个单位长度,得到的抛物线的顶点坐标为( )
A.(5,4)
B.(1,4)
C.(1,1)
D.(5,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x3y﹣xy3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家与学校在同一直线上且相距720m,一天早上他和弟弟都匀速步行去上学,弟弟走得慢,先走1分钟后,小明才出发,已知小明的速度是80m/分,以小明出发开始计时,设时间为x(分),兄弟两人之间的距离为ym,图中的折线是y与x的函数关系的部分图象,根据图象解决下列问题:
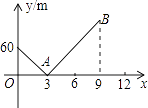
(1)弟弟步行的速度是m/分,点B的坐标是;
(2)线段AB所表示的y与x的函数关系式是;
(3)试在图中补全点B以后的图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】一台洗衣机的进价是2000元,如果商店要盈利10%,则购买m台这样的洗衣机需要元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y1=x和直线l2:y2=﹣2x+6相交于点A,直线l2与x轴交于点B,动点P沿路线O→A→B运动.
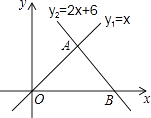
(1)求点A的坐标,并回答当x取何值时y1>y2?
(2)求△AOB的面积;
(3)当△POB的面积是△AOB的面积的一半时,求出这时点P的坐标.
相关试题

