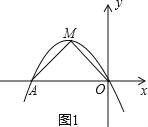
【题目】已知抛物线C1:y=ax2+4ax+4a+b(a≠0,b>0)的顶点为M,经过原点O且与x轴另一交点为A.
(1)求点A的坐标;
(2)若△AMO为等腰直角三角形,求抛物线C1的解析式;
(3)现将抛物线C1绕着点P(m,0)旋转180°后得到抛物线C2,若抛物线C2的顶点为N,当b=1,且顶点N在抛物线C1上时,求m的值.
参考答案:
【答案】(1)、(-4,0);(2)、y=﹣![]() x2﹣2x;(3)、m=﹣2+
x2﹣2x;(3)、m=﹣2+![]() 或﹣2﹣
或﹣2﹣![]()
【解析】
试题分析:(1)、由抛物线经过原点可知当x=0时,y=0,由此可得关于x的一元二次方程,解方程即可求出抛物线x轴另一交点坐标;(2)、由△AMO为等腰直角三角形,抛物线的顶点为M,可求出b的值,再把原点坐标(0,0)代入求出a的值,即可求出抛物线C1的解析式;(3)、由b=1,易求线抛物线C1的解析式,设N(n,﹣1),再由点P(m,0)可求出n和m的关系,当顶点N在抛物线C1上可把N的坐标代入抛物线即可求出m的值.
试题解析:(1)、∵抛物线C1:y=ax2+4ax+4a+b(a≠0,b>0)经过原点O, ∴0=4a+b,
∴当ax2+4ax+4a+b=0时,则ax2+4ax=0, 解得:x=0或﹣4,∴抛物线与x轴另一交点A坐标是(﹣4,0);
(2)、∵抛物线C1:y=ax2+4ax+4a+b=a(x+2)2+b(a≠0,b>0),(如图1) ∴顶点M坐标为(﹣2,b),
∵△AMO为等腰直角三角形, ∴b=2, ∵抛物线C1:y=ax2+4ax+4a+b=a(x+2)2+b过原点,
∴a(0+2)2+2=0, 解得:a=﹣![]() , ∴抛物线C1:y=﹣
, ∴抛物线C1:y=﹣![]() x2﹣2x;
x2﹣2x;
(3)、∵b=1,抛物线C1:y=ax2+4ax+4a+b=a(x+2)2+b过原点,(如图2) ∴a=﹣![]() ,
,
∴y=﹣![]() (x+2)2+1=﹣
(x+2)2+1=﹣![]() x2﹣x, 设N(n,﹣1),又因为点P(m,0), ∴n﹣m=m+2,
x2﹣x, 设N(n,﹣1),又因为点P(m,0), ∴n﹣m=m+2,
∴n=2m+2 即点N的坐标是(2m+2,﹣1), ∵顶点N在抛物线C1上, ∴﹣1=﹣![]() (2m+2+2)2+1,
(2m+2+2)2+1,
解得:m=﹣2+![]() 或﹣2﹣
或﹣2﹣![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)请在横线上填写合适的内容,完成下面的证明:
如图1,AB∥CD,求证:∠B+∠D=∠BED.
证明:过点E引一条直线EF∥AB
∴∠B=∠BEF,( )
∵AB∥CD,EF∥AB
∴EF∥CD( )
∴∠D=( )
∴∠B+∠D=∠BEF+∠FED
即∠B+∠D=∠BED.
(2)如图2,AB∥CD,请写出∠B+∠BED+∠D=360°的推理过程.
(3)如图3,AB∥CD,请直接写出结果∠B+∠BEF+∠EFD+∠D=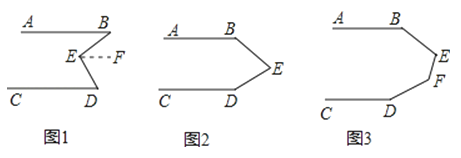
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于矩形的说法,正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.矩形的对角线相等且互相平分
D.矩形的对角线互相垂直且平分 -
科目: 来源: 题型:
查看答案和解析>>【题目】在长方体、圆柱、圆锥、球中,三视图均一样的几何体是_____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】据4月13日新华社报道,我国由陈薇院士组织的腺病毒载体重组新冠病毒疫苗率先进入第二期临床试验.我们从中选取甲、乙、丙三组各有7名志愿者,测得三组志愿者的体重数据的平均数都是58,方差分别为S甲2=36,S乙2=25,S丙2=16,则数据波动最小的一组是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】丽华根据演讲比赛中九位评委所给的分数作了如下表格:
平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A.平均数
B.众数
C.方差
D.中位数 -
科目: 来源: 题型:
查看答案和解析>>【题目】若(m+3)x|m|﹣2+5=0是关于x的一元一次方程,则m=_____.
相关试题

