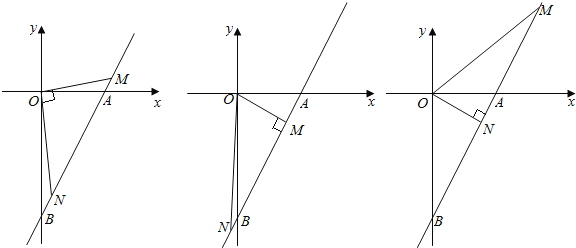
【题目】已知直线y=2x-5与x轴和y轴分别交于点A和点B,抛物线y=-x2+bx+c的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
(1)如图,当点M与点A重合时,求抛物线的解析式;
(2)在(1)的条件下,求点N的坐标和线段MN的长;
(3)抛物线y=-x2+bx+c在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)抛物线的解析式![]() ;
;
(2)点N的坐标为![]() ,线段MN的长为
,线段MN的长为![]() ;
;
(3)存在点M(2,-1),或(4,3)
【解析】试题分析:(1)①首先求得直线与x轴,y轴的交点坐标,利用二次函数的对称轴的公式即可求解;
②N在直线上同时在二次函数上,因而设N的横坐标是a,则在两个函数上对应的点的纵坐标相同,据此即可求得a的值,即N的坐标,过N作NC⊥x轴,垂足为C,利用勾股定理即可求得MN的长;
(2)△AOB的三边长可以求得OB=2OA,AB边上的高可以求得是![]() ,抛物线y=-x2+bx+c在直线AB上平移,则MN的长度不变,根据(1)的结果是2
,抛物线y=-x2+bx+c在直线AB上平移,则MN的长度不变,根据(1)的结果是2![]() ,MN是AB边上的高的二倍,当OM⊥AB或ON⊥AB时,两个三角形相似,据此即可求得M的坐标.
,MN是AB边上的高的二倍,当OM⊥AB或ON⊥AB时,两个三角形相似,据此即可求得M的坐标.
试题解析:(1)①∵直线y=2x-5与x轴和y轴交于点A和点B,
∴A(![]() ,0),B(0,-5).
,0),B(0,-5).
当顶点M与点A重合时,
∴M(![]() ,0).
,0).
∴抛物线的解析式是:y=(x![]() )2.即y=x2+5x
)2.即y=x2+5x![]() .
.
②∵N在直线y=2x-5上,设N(a,2a-5),又N在抛物线y=x2+5x![]() 上,
上,
∴2a5=a2+5a![]() .
.
解得a1=![]() ,a2=
,a2=![]() (舍去)
(舍去)
∴N(![]() ,4).
,4).
过N作NC⊥x轴,垂足为C.
∵N(![]() ,4),
,4),
∴C(![]() ,0).
,0).
∴NC=4.MC=OMOC=![]()
![]() =2.
=2.
∴MN=![]() ;
;
(2)设M(m,2m-5),N(n,2n-5).
∵A(![]() ,0),B(0,-5),
,0),B(0,-5),
∴OA=![]() ,OB=5,则OB=2OA,AB=
,OB=5,则OB=2OA,AB=![]() ,
,
当∠MON=90°时,∵AB≠MN,且MN和AB边上的高相等,因此△OMN与△AOB不能全等,
∴△OMN与△AOB不相似,不满足题意.
当∠OMN=90°时, ![]() ,即
,即![]() ,解得OM=
,解得OM=![]() ,
,
则m2+(2m-5)2=(![]() )2,解得m=2,
)2,解得m=2,
∴M(2,-1);
当∠ONM=90°时, ![]() ,即
,即![]() ,解得ON=
,解得ON=![]() ,
,
则n2+(2n-5)2=(![]() )2,解得n=2,
)2,解得n=2,
∵OM2=ON2+MN2,
即m2+(2m-5)2=5+(2![]() )2,
)2,
解得:m=4,
则M的坐标是M(4,3).
故M的坐标是:(2,-1)或(4,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:
价格x(元/个)
…
30
40
50
60
…
销售量y(万个)
…
5
4
3
2
…
同时,销售过程中的其他开支(不含进价)总计40万元.
(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】知识链接:将两个含30°角的全等三角尺放在一起,让两个30°角合在一起成60°,经过拼凑、观察、思考,探究出“直角三角形中30°角所对的直角边等于斜边的一半”结论.
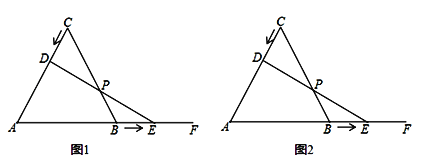
如图:等边三角形ABC的边长为4cm,点D从点C出发沿CA向A运动,点E从B出发沿AB的延长线BF向右运动,已知点D、E都以每秒0.5cm的速度同时开始运动,运动过程中DE与BC相交于点P,设运动时间为x秒.
(1)请直接写出AD长.(用x的代数式表示)
(2)当△ADE为直角三角形时,运动时间为几秒?
(2)求证:在运动过程中,点P始终为线段DE的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(﹣1,2)关于y轴的对称点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形的两边长分别为2和5,则第三边长可能是( )
A.2
B.3
C.5
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知am=2,an=3,求a3m+2n的值;
(2)已知a-b=4,ab=3,求a2-5ab+b2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读,再因式分解:x4+4=(x4+4x2+4)-4x2=(x2+2)2-(2x)2=(x2-2x+2)(x2+2x+2),按照这种方法把多项式x4+64因式分解.
相关试题

