Question

【题目】某公司销售一种进价为20元/个的计算器，其销售量y（万个）与销售价格x（元/个）的变化如下表：

价格x（元/个）	…	30	40	50	60	…
销售量y（万个）	…	5	4	3	2	…

同时，销售过程中的其他开支（不含进价）总计40万元．

（1）观察并分析表中的y与x之间的对应关系，用所学过的一次函数，反比例函数或二次函数的有关知识写出y（万个）与x（元/个）的函数解析式．

（2）求出该公司销售这种计算器的净得利润z（万元）与销售价格x（元/个）的函数解析式，销售价格定为多少元时净得利润最大，最大值是多少？

（3）该公司要求净得利润不能低于40万元，请写出销售价格x（元/个）的取值范围，若还需考虑销售量尽可能大，销售价格应定为多少元？

Answer 1

【答案】解：（1）根据表格中数据可得出：y与x是一次函数关系，设解析式为：y=ax+b，

则，解得： 。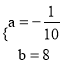

∴函数解析式为：y=x+8。

（2）根据题意得：

z=（x﹣20）y﹣40=（x﹣20）（x+8）﹣40=x2+10x﹣200=（x2﹣100x）﹣200

= [（x﹣50）2﹣2500]﹣200=（x﹣50）2+50，

∵＜0，∴x=50，z最大=50。

∴该公司销售这种计算器的净得利润z与销售价格x）的函数解析式为z=x2+10x﹣200，销售价格定为50元/个时净得利润最大，最大值是50万元。

（3）当公司要求净得利润为40万元时，即（x﹣50）2+50=40，解得：x1=40，x2=60。

作函数图象的草图，

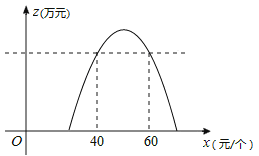
通过观察函数y=（x﹣50）2+50的图象，可知按照公司要求使净得利润不低于40万元，则销售价格的取值范围为：40≤x≤60．

而y与x的函数关系式为：y=x+8，y随x的增大而减少，

∴若还需考虑销售量尽可能大，销售价格应定为40元/个。

【解析】试题分析：（1）根据数据得出y与x是一次函数关系，进而利用待定系数法求一次函数解析式。

（2）根据z=（x﹣20）y﹣40得出z与x的函数关系式，应用二次函数最值原理求解即可。

（3）首先求出40=（x﹣50）2+50时x的值，从而二次函数的性质根据得出x（元/个）的取值范围，结合一次函数的性质即可求得结果。