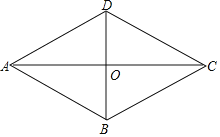
【题目】如图,在四边形ABCD中,AD∥BC,CA平分∠DCB,DB平分∠ADC
(1)求证:四边形ABCD是菱形;
(2)若AC=8,BD=6,求点D到AB的距离
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由平行线的性质和角平分线的性质可得AD=BC,且AD∥BC,可证四边形ABCD是平行四边形,且AD=CD,可证四边形ABCD是菱形;
(2)由勾股定理可求AB的长,由面积法可求点D到AB的距离.
证明:(1)∵CA平分∠DCB,DB平分∠ADC
∴∠ADB=∠CDB,∠ACD=∠ACB
∵AD∥BC
∴∠DAC=∠ACB=∠ACD,∠ADB=∠DBC=∠CDB
∴AD=CD,BC=CD
∴AD=BC,且AD∥BC
∴四边形ABCD是平行四边形,且AD=CD
∴四边形ABCD是菱形
(2)如图,过点D作DE⊥AB,
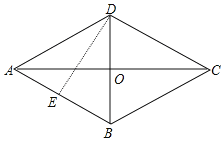
∵四边形ABCD是菱形
∴AO=CO=4,BO=DO=3,AC⊥BD
∴AB=![]() =
=![]() =5
=5
∵S△ABD=![]() AB×DE=
AB×DE=![]() ×DB×AO
×DB×AO
∴5DE=6×4
∴DE=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】南通市体育中考女生现场考试内容有三项:第一项200米跑、实心球、三级蛙跳(三选一);第二项双杠、仰卧起坐、跳绳(三选一);第三项篮球、排球、足球(三选一).小卉同学选择200米跑,双杠和篮球.小华同学第一项决定选200米跑,第二项和第三项的选择待定.
(1)请问小华同学第一项决定选200米跑的情况下有 种选择方案;
(2)用画树状图或列表的方法求小华和小卉同学在三项的选择中至少有两项方案选择一样的概率.(友情提酲:各种方案用A、B、C、…或①、②、③、…等符号来代表可简化解答过程)
-
科目: 来源: 题型:
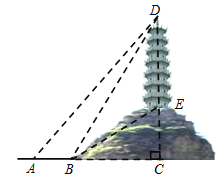
查看答案和解析>>【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)
-
科目: 来源: 题型:
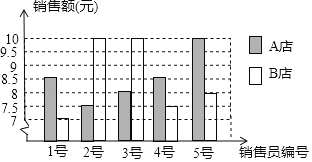
查看答案和解析>>【题目】A、B两店分另选5名销售员某月的销售额(单位:万元)进行分析,数据如下图表(不完整):
平均数
中位数
众数
A店
8.5
B店
8
10
(1)根据图a数据填充表格b所缺的数据;
(2)如果A店想让一半以上的销售员达到销售目标,你认为月销售额定为多少合适?说明理由.
-
科目: 来源: 题型:
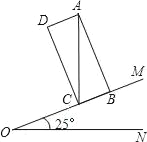
查看答案和解析>>【题目】如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
(1)求∠ACD度数;
(2)当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,某校对部分学生及家长就校园安全知识的了解程度,进行了随机抽样调查,并绘制成如图所示的两幅统计图
 不完整
不完整 根据统计图中的信息,若全校有2050名学生,请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生人数为
根据统计图中的信息,若全校有2050名学生,请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生人数为

A.1330B.1350C.1682D.1850
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知同一平面内,∠AOB=90°,∠AOC=30°,
(1)画出图形并求∠COB的度数;
(2)若OD平分∠BOC,OE平分∠AOC,求∠DOE的度数.
相关试题

