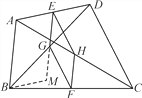
【题目】在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,当AB、CD满足什么条件时,四边形EGFH是菱形?请证明你的结论.(提示:过点B作BM∥AD交EG的延长线于点M,证明EG//AB且EG=![]() AB)
AB)
参考答案:
【答案】见解析
【解析】试题分析:本题可根据菱形的定义来求解.E、G分别是AD,BD的中点,那么EG就是三角形ADB的中位线,同理,HF是三角形ABC的中位线,因此EG、HF同时平行且相等于AB,因此EG∥HF,EG=HF.因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH=![]() CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件.
试题解析:当AB=CD时,四边形EGFH为菱形.
证明:过点B作BM∥AD交EG的延长线于点M,则∠DEG=∠GMB.∵G为BD的中点,∴DG=GB.
又∵∠DGE=∠BGM,∴△DGE≌△BGM,∴EG=GM,ED=BM.
∵E为AD的中点,∴AE=ED,∴BM∥AE,
∴四边形AEMB为平行四边形,
∴EM∥AB,
∴EG∥![]() AB,EG=
AB,EG=![]() AB.
AB.
同理FH∥![]() CD,GF∥
CD,GF∥![]() CD,GF=
CD,GF=![]() CD,
CD,
∴四边形EGFH为平行四边形.
∵AB=CD,∴GF=HF,
∴平行四边形EGHF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:
定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加、减,乘法运算与整式的加、减、乘法运算类似.
例如计算:(2-i)+(5+3i)=(2+5)+(-1+3)i=7+2i;
(1+i)×(2-i)=1×2-i+2×i-i2=2+(-1+2)i+1=3+i;
根据以上信息,完成下列问题:
(1)填空:i3= ,i4= ;
(2)计算:(1+i)×(3-4i);
(3)计算:i+i2+i3+…+i2018.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
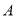 是双曲线
是双曲线 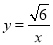 在第三象限分支上的一个动点,连接
在第三象限分支上的一个动点,连接 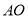 并延长交另一分支于点
并延长交另一分支于点 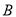 ,以
,以 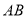 为边作等边三角形
为边作等边三角形  ,点
,点 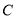 在第四象限内,且随着点
在第四象限内,且随着点 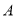 的运动,点
的运动,点 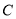 的位置也在不断变化,但点
的位置也在不断变化,但点 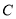 始终在双曲线
始终在双曲线 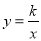 上运动,则
上运动,则 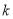 的值是_______________.
的值是_______________.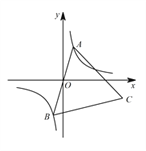
-
科目: 来源: 题型:
查看答案和解析>>【题目】何老师安排喜欢探究问题的小明解决某个问题前,先让小明看了一个有解答过程的例题.
例:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0∴m=﹣3,n=3
为什么要对2n2进行了拆项呢?
聪明的小明理解了例题解决问题的方法,很快解决了下面两个问题.相信你也能很好的解决下面的这两个问题,请写出你的解题过程..
解决问题:
(1)若x2﹣4xy+5y2+2y+1=0,求xy的值;
(2)已知a、b、c是△ABC的三边长,满足a2+b2=10a+12b﹣61,c是△ABC中最短边的边长,且c为整数,那么c可能是哪几个数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表所示为装运、销售甲、乙、丙三种蔬菜的重量及利润。某公司计划用20辆汽车装运甲、乙、丙三种蔬菜共36吨到某地销售.规定每辆汽车满载,每车只装一种蔬菜,每种蔬菜不少于一车。应如何安排,可使公司获得利润18300元?
甲
乙
丙
每辆汽车装运的吨数
2
1
1.5
每吨蔬菜可获利润(百元)
5
7
4
-
科目: 来源: 题型:
查看答案和解析>>【题目】为贯彻政府报告中“大众创业、万众创新”的精神,某镇对辖区内所有的小微企业按年利润w(万元)的多少分为以下四个类型:A类(w<10),B类(10≤w<20),C类(20≤w<30),D类(w≥30),该镇政府对辖区内所有小微企业的相关信息进行统计后,绘制成以下条形统计图和扇形统计图,请你结合图中信息解答下列问题:

(1)该镇本次统计的小微企业总个数是 ,扇形统计图中B类所对应扇形圆心角的度数为 度,请补全条形统计图;
(2)为了进一步解决小微企业在发展中的问题,该镇政府准备召开一次座谈会,每个企业派一名代表参会.计划从D类企业的4个参会代表中随机抽取2个发言,D类企业的4个参会代表中有2个来自高新区,另2个来自开发区.请用列表或画树状图的方法求出所抽取的2个发言代表都来自高新区的概率.
相关试题

