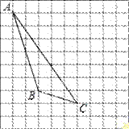
【题目】如图,在方格纸内将△ABC水平向右平移4个单位,再向下后平移1得到△A′B′C′.
(1)画出平移后的△A′B′C′;
(2)画出AB边上的高线CD(利用三角板画图);
(3)画出△ABC中AB边上的中线CE;
(4)图中AC与A′C′的关系是: ;
(5)△BCE的面积为 .
(6)若△A″BC的面积与△ABC面积相同,则A″(A″在格点上)的位置(除A点外)共有_________个.
参考答案:
【答案】(1)(2)(3)略(4)平行且相等(5)4(6)3
【解析】
(1)分别作出点A、B、C向右平移4个单位,再向下后平移1得到的对应点,顺次连接即可得;
(2)根据三角形高的定义作出线段可得;
(3)根据三角形中线的定义作出线段可得;
(4)根据平移的性质即可得;
(5)利用割补法求解可得;
(6)根据两三角形的底边公共,而面积相等知点A″应位于过点A且平行于BC的直线上,据此可得.
(1)如图,△A′B′C′即为所求;

(2)如图,线段CD即为所求;
(3)如图,线段CE即为所求;
(4)图中AC与A′C′平行且相等,
故答案为:平行且相等;
(5)S△BCE=![]() ×4×4-
×4×4-![]() ×1×3-1×1-
×1×3-1×1-![]() ×1×3=4;
×1×3=4;
(6)若△A″BC的面积与△ABC面积相同,
则点A″应位于过点A且平行于BC的直线上,由图可知,这样的格点A″共有3个,
故答案为:3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】课本中有一个例题:
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2 .
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题: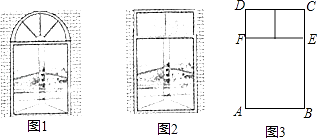
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=
 (∠BAC﹣∠C);④∠BGH=∠ABE+∠C.
(∠BAC﹣∠C);④∠BGH=∠ABE+∠C.其中正确的是( )

A. ①②③ B. ①③④ C. ①②④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AB=4,BC=6.将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是( )

A.6
B.3
C.2.5
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C,E是直线l两侧的点,以C为圆心,CE长为半径画弧交l于A,B两点,又分别以A,B为圆心,大于
 AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,下列结论不一定正确的是( )
AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,下列结论不一定正确的是( ) 
A.CD⊥l
B.点A,B关于直线CD对称
C.点C,D关于直线l对称
D.CD平分∠ACB -
科目: 来源: 题型:
查看答案和解析>>【题目】任意一条线段EF,其垂直平分线的尺规作图痕迹如图所示.若连接EH,HF,FG,GE,则下列结论中,不一定正确的是( )
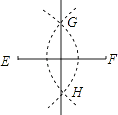
A.△EGH为等腰三角形
B.△EGF为等边三角形
C.四边形EGFH为菱形
D.△EHF为等腰三角形
相关试题

