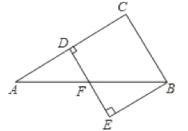
【题目】如图.△ABC中,AC的垂直平分线分别交AC、AB于点D. F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是_____
参考答案:
【答案】2![]()
【解析】
由AF=BF得到F为AB的中点,又DF垂直平分AC,得到D为AC的中点,可得出DF为三角形ABC的中位线,根据三角形中位线定理得到DF平行于CB,且DF等于BC的一半,由BC的长求出DF的长,由两直线平行同旁内角互补得到∠C=90°,同时由DE与EB垂直,ED与DC垂直,根据垂直的定义得到两个角都为直角,利用三个角为直角的四边形为矩形得到四边形BCDE为矩形,在直角三角形ADF中,利用锐角三角函数定义及特殊角的三角函数值,由∠A=30°,DF的长,求出AD的长,即为DC的长,由矩形的长BC于宽CD的乘积即可求出矩形BCED的面积.
∵AF=BF,即F为AB的中点,又DE垂直平分AC,即D为AC的中点,
∴DF为三角形ABC的中位线,
∴DE∥BC,DF=![]() BC,
BC,
又∠ADF=90°,
∴∠C=∠ADF=90°,
又BE⊥DE,DE⊥AC,
∴∠CDE=∠E=90°,
∴四边形BCDE为矩形,
∵BC=2,∴DF=![]() BC=1,
BC=1,
在Rt△ADF中,∠A=30°,DF=1,
∴tan30°=![]() ,即AD=
,即AD=![]() ,
,
∴CD=AD=![]() ,
,
则矩形BCDE的面积S=CDBC=2![]() .
.
故答案为:2![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年4月23日,是第23个世界读书日.为了推进中华传统文化教育,营造浓厚的读书氛围,我市某学校举办了“让读书成为习惯,让书香溢病校园”主题活动.为了解学生每周阅读时间,该校随机抽取了部分学生进行调查,根据调查结果,将阅诙时间
 (单位:小时)分成了
(单位:小时)分成了 组,
组, 

 ,下图是根据这组数据绘制的两幅不完整的统计图.请你结合图中所给信息解答下列问题:
,下图是根据这组数据绘制的两幅不完整的统计图.请你结合图中所给信息解答下列问题:
(1)这次随机抽取了 名学生进行调查;
(2)补全频数分布直方图;
(3)计算扇形统计图中扇形
 的圆心角的度数;
的圆心角的度数;(4)若该校共有
 名学生,请你估计每周阅读时间不足
名学生,请你估计每周阅读时间不足 小时的学生共有多少名?
小时的学生共有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】有依次排列的3个数:3,9,8,对任相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:3,6,9,
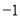 ,8,这称为第一次操作;做第二次同样的操作后也可产生一个新数串:3,3,6,3,9,
,8,这称为第一次操作;做第二次同样的操作后也可产生一个新数串:3,3,6,3,9,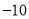 ,
,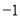 ,9,8,继续依次操作下去,问:从数串3,9,8开始操作第一百次以后所产生的那个新数串的所有数之和是多少?
,9,8,继续依次操作下去,问:从数串3,9,8开始操作第一百次以后所产生的那个新数串的所有数之和是多少? -
科目: 来源: 题型:
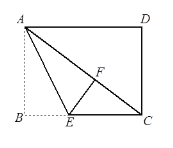
查看答案和解析>>【题目】如图,已知在长方形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上,若BE=3,EC=5,则线段CD的长是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)如图,直线y=x+m和抛物线y=
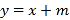 +bx+c都经过点A(1,0),
+bx+c都经过点A(1,0),B(3,2).
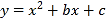
(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
-
科目: 来源: 题型:
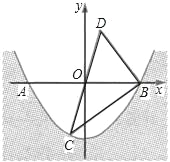
查看答案和解析>>【题目】某水渠的横截面呈抛物线,水面的宽度为AB(单位:米),现以AB所在直线为x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,设坐标原点为O.已知AB=8米,设抛物线解析式为y=ax2﹣4.
(1)求a的值;
(2)点C(﹣1,m)是抛物线上一点,点C关于原点O的对称点为点D,连接CD,BC,BD,求△BCD的面积.
相关试题

