【题目】探索与应用.先填写下表,通过观察后再回答问题:
a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| … | 0.01 | x | 1 | y | 100 | … |
(1)表格中x= ;y= ;
(2)从表格中探究a与![]() 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知![]() ≈3.16,则
≈3.16,则![]() ≈ ;②已知
≈ ;②已知![]() =1.8,若
=1.8,若![]() =180,则a= ;
=180,则a= ;
(3)拓展:已知![]() ,若
,若![]() ,则b= .
,则b= .
参考答案:
【答案】(1)0.1,10;(2)31.6,32400;(3)0.012.
【解析】
(1)由表格得出规律,求出x与y的值即可;
(2)根据算术平方根的被开方数扩大100倍,算术平方根扩大10倍,可得答案;
(3)根据立方根的被开方数缩小1000倍,立方根缩小10倍,可得答案.
(1)x=0.1,y=10,故答案为:0.1,10;
(2)①∵![]() ≈3.16,
≈3.16,
∴![]() =31.6,
=31.6,
②![]() =1.8,
=1.8,
∴a=32400,
故答案为:31.6,32400;
(4)∵![]() ,
,
∴b=0.012,故答案为:0.012.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=﹣
 x+m交折线OAB于点E.
x+m交折线OAB于点E.(1)请写出m的取值范围 ;
(2)记△ODE的面积为S,求S与m的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒跳动一个单位,那么第 2020 秒时跳蚤所在位置的坐标是( )

A.(5,44)B.(4,44)C.(4,45)D.(5,45)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB和∠COD的两边分别互相垂直,且∠COD比∠AOB的3倍少60°,则∠COD的度数为_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系,△ABC的三个顶点都在网格的格点上.
(1)把△ABC向下平移6个单位长度,再向左平移5个单位长度,得到△A1B1C1.请直接写出点A1、点B1和点C1的坐标.(不需要画图)
(2)求△ABC的面积.
(3)点D的坐标为(-3,1),在坐标轴上是否存在点E使得△BDE的面积等于△ABC的面积,若存在,请直接写出点E的坐标,若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2.求证:∠3=∠ACB.
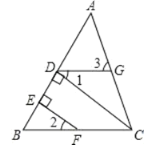
下面给出了部分证明过程和理由,请补全所有内容.
证明:∵CD⊥AB,FE⊥AB
∴∠BDC=∠BEF=90°( )
∴EF∥DC( )
∴∠2= ( )
又∵∠2=∠1(已知)
∴∠1= (等量代换)
∴DG∥BC( )
∴∠3=∠ACB(两直线平行,同位角相等)
-
科目: 来源: 题型:
查看答案和解析>>【题目】南湖公园有很多的长方形草地,草地里修了很多有趣的小路,下面三个图形都是长为50米,宽为30米的长方形草地,且小路的宽都是1米.
①如图1,阴影部分为1米宽的小路,长方形除去阴影部分后剩余部分为草地,则草地的面积为 ;
②如图2,有两条宽均为1米的小路(图中阴影部分),求草地的面积.
③如图3,非阴影部分为1米宽的小路,沿着小路的中间从入口E处走到出口F处,所走的路线(图中虚线)长为 .

相关试题

