【题目】如图,直线1上有A,B两点,AB=12cm,点O是线段AB上的一点,OA=2OB.
(1)OA=______cm,OB=______cm;
(2)若点C是线段AB上一点(点C不与点AB重合),且满足AC=CO+CB,求CO的长;
(3)若动点P,Q分别从A,B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s.设运动时间为t(s),当点P与点Q重合时,P,Q两点停止运动.求当t为何值时,2OP-OQ=4(cm);
![]()
参考答案:
【答案】(1)8,4;(2)CO的长是![]() ;(3)当t为1.6s或8s时,2OP-OQ=4.
;(3)当t为1.6s或8s时,2OP-OQ=4.
【解析】
(1)由于AB=12cm,点O是线段AB上的一点,OA=2OB,则OA+OB=3OB=AB=12cm,依此即可求解;
(2)根据图形可知,点C是线段AO上的一点,可设C点所表示的实数为x,分两种情况:①点C在线段OA上时,则x<0,②点C在线段OB上时,则x>0,根据AC=CO+CB,列出方程求解即可;
(3)分0≤t<4;4≤t≤12两种情况讨论求解即可.
解:(1)∵AB=12cm,OA=2OB,
∴OA+OB=3OB=AB=12cm,解得OB=4cm,
OA=2OB=8cm.
故答案为:8,4;
(2)设O点表示的数是0,C点所表示的实数为x,
分两种情况:①点C在线段OA上时,则x<0,
∵AC=CO+CB,
∴8+x=-x+4-x,
3x=-4,
x=![]() ;
;
②点C在线段OB上时,则x>0,
∵AC=CO+CB,
∴8+x=4,
x=-4(不符合题意,舍).
故CO的长是![]() ;
;
(3)当0≤t<4时,依题意有
2(8-2t)-(4+t)=4,
解得t=1.6;
当4≤t≤12时,依题意有
2(2t-8)-(4+t)=4,
解得t=8.
故当t为1.6s或8s时,2OP-OQ=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )

A. =
= 
B. =
= 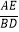
C. =
= 
D. =
= 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形纸片ABC中,点D在边AB(不包含端点A、B)上运动,连接CD,将∠ADC对折,点A落在直线CD上的点A′处,得到折痕DE;将∠BDC对折,点B落在直线CD上的点B′处,得到折痕DF.
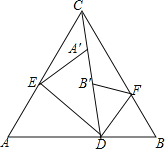
(1)若∠ADC=80°,求∠BDF的度数;
(2)试问∠EDF的大小是否会随着点D的运动而变化?若不变,求出∠EDF的大小;若变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
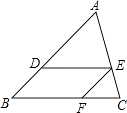
A.6
B.8
C.10
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A在数轴上和原点相距3个单位长度,点B在数轴上和原点相距
 个单位长度,则A、B两点这间的距离是 .
个单位长度,则A、B两点这间的距离是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
相关试题

