搜索
【题目】已知：
，点
，
分别在
，
上，点
为，之间的一点，连接
，
.
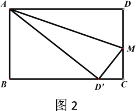
（1）如图1，求证：
；
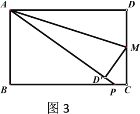
（2）如图2，
，
，
，
分别为
，
，
，
的角平分线，求证
与
互补；
图1. 
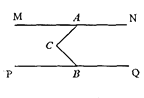图2.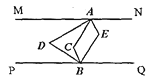 
参考答案：
【答案】（1）见解析，（2）见解析.
【解析】
（1）过C点作CG∥MN，再根据两直线平行，内错角相等即可证明；
（2）由（1）可知 
，
，再根据角平分线的性质与平角的性质知∠DAE=∠DBE=90°，即可证得
+
=180°.
解：（1）过C点作CG∥MN，
∵
，
∴
，
∴∠MAC=∠ACG,∠PBC=∠GCB，
∵∠ACB=∠ACG+∠GCB，
∴∠ACB=∠MAC+∠PBC
（2）由（1）同理可知 ，
∵
，
，
，
分别为
，
，
，
的角平分线，
∴∠DAE=∠DBE=
=90°，
∴∠D+∠E=360°-（∠DAE+∠DBE）=180°，
∴与互补.
-
科目： 来源： 题型：
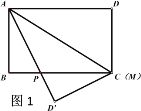
查看答案和解析>>【题目】已知长方形ABCD中，AD=10cm,AB=6cm,点M在边CD上，由C往D运动，速度为1cm/s，运动时间为t秒，将△ADM沿着AM翻折至△ADM，点D对应点为D，AD所在直线与边BC交于点P.
（1）如图1，当t=0时，求证：PA=PC；
（2）如图2，当t为何值时，点D恰好落在边BC上；
（3）如图3，当t=3时，求CP的长.
（ -
科目： 来源： 题型：
查看答案和解析>>【题目】甲组的
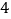名工人12月份完成的总工作量比此月人均定额的
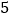倍多
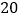件，乙组的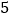名工人12月份完成的总工作量比此月人均定额的
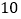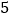倍少件.（1）如果两组工人实际完成的此月人均工作量相等，那么此月的人均定额是多少件？
（2）如果甲组工人实际完成的此月人均工作量比乙组工人实际完成的此月人均工作量少3件，那么此月人均定额是多少件？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，直线l1：
与坐标轴交于A，B两点，直线l2：
（
≠0）与坐标轴交于点C，D.（1）求点A，B的坐标；
（2）如图，当
=2时，直线l1，l2与相交于点E，求两条直线与
轴围成的△BDE的面积；（3）若直线l1，l2与
轴不能围成三角形，点P（a，b）在直线l2：（k≠0）上，且点P在第一象限.①求
的值；②若
,，求
的取值范围.
-
科目： 来源： 题型：
查看答案和解析>>【题目】用恰当的方法解下列方程：
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥DF，交AB于点E，连结EG、EF．
（1）求证：BG＝CF．
（2）请你判断BE+CF与EF的大小关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
（2） 如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.
相关试题
