【题目】如图,直线AB与y轴交于点A,与x轴交于点B,点A的纵坐标、点B的横坐标如图所示.
(1)求直线AB对应的函数表达式;
(2)点P在直线AB上,是否存在点P使得三角形AOP的面积为1,如果存在,求出所有满足条件的点P的坐标.

参考答案:
【答案】(1)y=-![]() x+2(2)(1,1.5)或(-1,2.5)
x+2(2)(1,1.5)或(-1,2.5)
【解析】试题(1)根据题意确定出A与B的坐标,设直线AB的解析式为y=kx+b(k≠0),将A与B坐标代入求出k与b的值,即可确定出直线AB解析式;
(2)设P横坐标为a,三角形AOP以OA为底边,a的绝对值为高,由此表示出三角形APO的面积,根据已知面积求出a的值,结合点P在直线AB上,即可确定出P点的坐标.
试题解析:(1)根据题意得A(0,2),B(4,0),
设直线AB的解析式为y=kx+b(k≠0),
则![]() ,
,
∴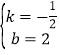 ,
,
(2)存在点P使得三角形AOP的面积为1.
设点P的横坐标为a,根据题意得S△AOP=![]() OA·|a|=|a|=1,
OA·|a|=|a|=1,
解得a=1或a=-1,
则点P的坐标为(1,1.5)或(-1,2.5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,CD⊥AB于点D,CD=BD.BE平分∠ABC,点H是BC边的中点.连接DH,交BE于点G.连接CG.
(1)求证:△ADC≌△FDB;
(2)求证:
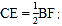
(3)判断△ECG的形状,并证明你的结论.
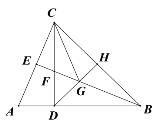
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一列数-1,2,-1,2,2,-1,2,2,2,-1,…其中相邻的两个-1被2隔开,第n对-1之问有n个2,则第21个数是______,这一列数的前2019个数的和为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】黄冈农科院培育的“黄金8号”玉米种子的价格为5元/kg,如果一次购买2kg以上的种子,超过2kg部分的种子的价格打8折.
(Ⅰ)根据题意,填写下表:
购买种子的数量/kg 1.5 2 3.5 4 …
付款金额/元 7.5 16 …
(Ⅱ)设购买种子数量为xkg,付款金额为y元,求y关于x的函数解析式;
(Ⅲ)若小明帮奶奶一次购买该种子花费了30元,求他购买种子的数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=
 则∠BOC=_______,∠AOM=_______,∠BON=_________;
则∠BOC=_______,∠AOM=_______,∠BON=_________;(2)若∠AOC=
 则∠BON=_______(用含有
则∠BON=_______(用含有 的式子表示);
的式子表示);(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变,若∠AOC=
 (
( 为钝角),求∠BON的度数(用含
为钝角),求∠BON的度数(用含 的式子表示).
的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,现有5张写着不同数字的卡片,请按要求完成下列问题:

 若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______. 若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______. 若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:(
 ﹣
﹣ )2+(2
)2+(2 +
+ )(2
)(2 ﹣
﹣ )
)(2)因式分解:9a2(x﹣y)+4b2(y﹣x)
(3)先化简,再求值:
 ÷(a﹣1﹣
÷(a﹣1﹣ ),其中a2﹣a﹣6=0.
),其中a2﹣a﹣6=0.
相关试题

