【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=![]() 则∠BOC=_______,∠AOM=_______,∠BON=_________;
则∠BOC=_______,∠AOM=_______,∠BON=_________;
(2)若∠AOC=![]() 则∠BON=_______(用含有
则∠BON=_______(用含有![]() 的式子表示);
的式子表示);
(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变,若∠AOC=![]() (
(![]() 为钝角),求∠BON的度数(用含
为钝角),求∠BON的度数(用含![]() 的式子表示).
的式子表示).

参考答案:
【答案】(1)59°40′; 29°20′; 60°40′; (2)2α;
(3)360°-2α.
【解析】
(1)根据∠BOC=∠AOB-∠AOC进行计算即可,
由OC平分∠MOB得∠BOM=2∠BOC,则∠AOM=∠BOM-∠AOB,
∠BON=180°-∠BOM,代入计算即可得出答案;
(2)仿照(1)中方法,先求出∠BOC,再求得∠BOM,最后再代入∠BON=180°-∠BOM化简即可;
(3)由图可知∠BOC=∠AOC-∠AOB,然后由角平分线定义得∠BOM=2∠BOC,最后代入∠BON=180°-∠BOM化简即可得出答案.
解:(1)∠BOC=∠AOB-∠AOC
=90°-30°20′
=59°40′,
∵OC平分∠MOB,
∴∠BOM=2∠BOC=2×59°40′=119°20′,
∴∠AOM=∠BOM-∠AOB
=119°20′-90°
=29°20′,
∠BON=180°-∠BOM
=180°-119°20′
=60°40′.
故答案为:59°40′,29°20′,60°40′;
(2)∠BOC=∠AOB-∠AOC=90°-α,
∵OC平分∠MOB,
∴∠BOM=2∠BOC=2(90°-α)=180°-2α,
∴∠BON=180°-∠BOM
=180°-(180°-2α)
=2α.
故答案为:2α;
(3)由图可知∠BOC=∠AOC-∠AOB=α-90°,
∵OC平分∠MOB,
∴∠BOM=2∠BOC=2(α-90°)= 2α-180°,
∴∠BON=180°-∠BOM
=180°-(2α-180°)
=360°-2α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y-4与x成正比,当x=1时,y=2
(1)求y与x之间的函数关系式,在下列坐标系中画出函数图象;
(2)当x=
 时,求函数y的值;
时,求函数y的值;(3)结合图象和函数的增减性,求当y<-2时自变量x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
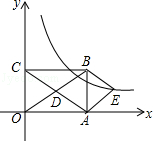
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】宁波轨道交通4号线已开工建设,计划2020年通车试运营.为了了解镇民对4号线地铁票的定价意向,某镇某校数学兴趣小组开展了“你认为宁波4号地铁起步价定为多少合适”的问卷调查,并将调查结果整理后制成了如下统计图,根据图中所给出的信息解答下列问题:
(1)求本次调查中该兴趣小组随机调查的人数;
(2)请你把条形统计图补充完整;
(3)如果在该镇随机咨询一位居民,那么该居民支持“起步价为2元或3元”的概率是
(4)假设该镇有3万人,请估计该镇支持“起步价为3元”的居民大约有多少人?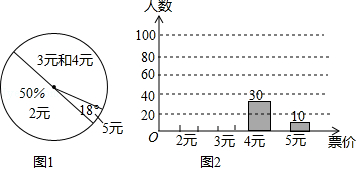
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=
 ∠A.
∠A. 
(1)求证:BC是⊙O的切线;
(2)若sinB=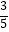 ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】
国际比赛的足球场长在100m到110m之间,宽在64m到75m之间,为了迎接2015年的亚洲杯,某地建设了一个长方形的足球场,其长是宽的1.5倍,面积是7560m2.请你判断这个足球场能用于国际比赛吗?并说明理由.
-
科目: 来源: 题型:
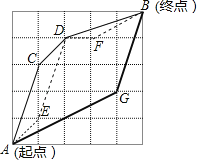
查看答案和解析>>【题目】嘉嘉参加机器人设计活动,需操控机器人在5×5的方格棋盘上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1,R2,R3,其行经位置如图与表所示:
路径
编号
图例
行径位置
第一条路径
R1
_
A→C→D→B
第二条路径
R2
…
A→E→D→F→B
第三条路径
R3
▂
A→G→B
已知A、B、C、D、E、F、G七点皆落在格线的交点上,且两点之间的路径皆为直线,在无法使用任何工具测量的条件下,请判断R1、R2、R3这三条路径中,最长与最短的路径分别为何?请写出你的答案,并完整说明理由.
相关试题

