搜索
【题目】(1)计算：(
﹣
)2+(2+
)(2﹣)
(2)因式分解：9a2(x﹣y)+4b2(y﹣x)
(3)先化简，再求值：
÷(a﹣1﹣
)，其中a2﹣a﹣6=0．
参考答案：
【答案】（1）11﹣2
；（2）（x﹣y）（3a+2b）（3a﹣2b）；（3）
，
【解析】
试题（1）（
﹣
）2运用完全平方公式计算，（2+）（2﹣）运用平方差公式计算，然后合并同类项或同类二次根式；
（2）先提公因式(x-y)，再运用平方差公式进行二次分解；
（3）先把括号内通分，再把除法转化为乘法，然后把分子、分母分解因式约分化简；把a2﹣a﹣6=0变形为a2﹣a=6，整体代入求值.
解：（1）原式=（）2﹣2×
×
+（）2+（2）2﹣（
）2
=2﹣2+3+12﹣6
=11﹣2；
（2）原式=9a2（x﹣y）﹣4b2（x﹣y）
=（x﹣y）（9a2﹣4b2）
=（x﹣y）（3a+2b）（3a﹣2b）；
（3）
÷（a﹣1﹣
）
=÷ 
=÷
=
=
=
，
∵a2﹣a﹣6=0，
∴a2﹣a=6，
∴原式=
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB与y轴交于点A，与x轴交于点B，点A的纵坐标、点B的横坐标如图所示．
(1)求直线AB对应的函数表达式；
(2)点P在直线AB上，是否存在点P使得三角形AOP的面积为1，如果存在，求出所有满足条件的点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=
则∠BOC=_______，∠AOM=_______，∠BON=_________；(2)若∠AOC=
则∠BON=_______(用含有
的式子表示)；(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变，若∠AOC=
(为钝角),求∠BON的度数(用含的式子表示).
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，现有5张写着不同数字的卡片，请按要求完成下列问题：
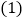若从中取出2张卡片，使这2张卡片上数字的乘积最大，则乘积的最大值是______．
若从中取出2张卡片，使这2张卡片上数字相除的商最小，则商的最小值是______．
若从中取出4张卡片，请运用所学的计算方法，写出两个不同的运算式，使四个数字的计算结果为24． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点B是线段AC上一点，AC=4AB，AB=6cm，直线MN经过线段BC的中点P．
（1）图中共有线段______条，图中共有射线______条．
（2）图中有______组对顶角，与∠MPC互补的角是______．
（3）线段AP的长度是______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】
（本小题满分8分）某学校组织八年级学生参加社会实践活动，若单独租用35座客车若干辆，则刚好坐满；若单独租用55座客车，则可以少租一辆，且余45个空座位．
（1）求该校八年级学生参加社会实践活动的人数；
（2）已知35座客车的租金为每辆320元，55座客车的租金为每辆400元．根据租车资金不超过1500元的预算，学校决定同时租用这两种客车共4辆（可以坐不满）．请你计算本次社会实践活动所需车辆的租金．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解答下列各题：
（1）x取何值时，代数式3x+2的值不大于代数式4x+3的值？（2）当m为何值时，关于x的方程
x-1=m的解不小于3？ （3）已知不等式2（x+3）-4＜0， 化简：︳4x+1︱-︱2-4x︱.
相关试题
