【题目】抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的一个交点
轴的一个交点![]() 在点
在点![]() 和
和![]() 之间,其部分图象如图所示,则以下结论:①
之间,其部分图象如图所示,则以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④方程以
;④方程以![]() 有两个的实根,其中正确的个数为( )
有两个的实根,其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】B
【解析】
抛物线开口向上a>0,对称轴在y轴左侧,b>0,抛物线和y轴负半轴相交,c<0,则abc<0,由抛物线与x轴有两个交点得到b2-4ac>0;有抛物线顶点坐标得到抛物线的对称轴为直线x=-1,则根据抛物线的对称性得抛物线与x轴的另一个交点在点(-3,0)和(-2,0)之间,所以当x=1时,y>0,则a+b+c>0;由抛物线的顶点为D(-1,-3)得a-b+c=-3,由抛物线的对称轴为直线![]() 得b=2a,所以a-c=3;根据二次函数的最值问题,当x=-1时,二次函数有最小值为-3,即b2-4ac=-12a,b2-4a(c+3)=b2-4ac-12a=-24a,所以说方程ax2+bx+c+3=0无实数根.
得b=2a,所以a-c=3;根据二次函数的最值问题,当x=-1时,二次函数有最小值为-3,即b2-4ac=-12a,b2-4a(c+3)=b2-4ac-12a=-24a,所以说方程ax2+bx+c+3=0无实数根.
∵抛物线开口向上,
∴a>0,
∵对称轴在y轴左侧,
∴b>0,
∵抛物线和y轴负半轴相交,
∴c<0,
∴abc<0,故①错误;
∵当x=1时,y>0,
∴y=a+b+c>0,故②错误;
∵抛物线的顶点为D(1,3)
∴ab+c=3,
∵抛物线的对称轴为直线![]() 得b=2a,
得b=2a,
把b=2a代入ab+c=3,得a2a+c=3,
∴ca=3,
∴ac=3,故③正确;
∵二次函数y=ax2+bx+c有最小值为3,
∴b24ac=12a,
∴方程ax2+bx+c+3=0的判别式△=b24a(c+3)=b24ac12a=0,
∴方程ax2+bx+c+3=0有两个相等的实数根,故④正确;
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, ,
, 于点E,
于点E, 于点D,BE与AD相交于F.
于点D,BE与AD相交于F. 求证:
求证: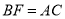 ;
; 若
若 ,求AF的长.
,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位需采购一批商品,购买甲商品10件和乙商品15件需资金350元,而购买甲商品15件和乙商品10件需要资金375元.
 求甲、乙商品每件各多少元?
求甲、乙商品每件各多少元? 本次计划采购甲、乙商品共30件,计划资金不超过460元,
本次计划采购甲、乙商品共30件,计划资金不超过460元, 最多可采购甲商品多少件?
最多可采购甲商品多少件? 若要求购买乙商品的数量不超过甲商品数量的
若要求购买乙商品的数量不超过甲商品数量的 ,请给出所有购买方案,并求出该单位购买这批商品最少要用多少资金.
,请给出所有购买方案,并求出该单位购买这批商品最少要用多少资金. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数的图象经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是【 】

A.y的最大值小于0 B.当x=0时,y的值大于1
C.当x=-1时,y的值大于1 D.当x=-3时,y的值小于0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
 的图象与
的图象与 轴的一个交点是
轴的一个交点是 ,顶点是
,顶点是 ,根据
,根据
图象回答下列问题:
 当
当 ________时,
________时, 随
随 的增大而增大;
的增大而增大; 方程
方程 的两个根为________,方程
的两个根为________,方程 的根为________;
的根为________; 不等式
不等式 的解集为________;
的解集为________; 若方程
若方程 无解,则
无解,则 的取值范围为________.
的取值范围为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是等边
 内一点
内一点 将
将 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转 得
得 ,连接
,连接 已知
已知
 .
. 求证:
求证: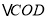 是等边三角形;
是等边三角形; 当
当 时,试判断
时,试判断 的形状,并说明理由;
的形状,并说明理由; 探究:当
探究:当 为多少度时,
为多少度时, 是等腰三角形.
是等腰三角形.
相关试题

