【题目】某单位需采购一批商品,购买甲商品10件和乙商品15件需资金350元,而购买甲商品15件和乙商品10件需要资金375元.
![]() 求甲、乙商品每件各多少元?
求甲、乙商品每件各多少元?
![]() 本次计划采购甲、乙商品共30件,计划资金不超过460元,
本次计划采购甲、乙商品共30件,计划资金不超过460元,
![]() 最多可采购甲商品多少件?
最多可采购甲商品多少件?
![]() 若要求购买乙商品的数量不超过甲商品数量的
若要求购买乙商品的数量不超过甲商品数量的![]() ,请给出所有购买方案,并求出该单位购买这批商品最少要用多少资金.
,请给出所有购买方案,并求出该单位购买这批商品最少要用多少资金.
参考答案:
【答案】(1)甲商品每件17元,乙商品每件12元;(2)①最多可采购甲商品20件;②购买方案有四种,
方案一:甲商品20件,乙商品10件,此时花费为:20×17+10×12=460(元);
方案二:甲商品19件,乙商品11件,此时花费为:19×17+11×12=455(元);
方案三:甲商品18件,乙商品12件,此时花费为:18×17+12×12=450(元);
方案四:甲商品17件,乙商品13件,此时花费为:17×17+13×12=445(元).
即购买甲商品17件,乙商品13件时花费最少,最少要用445元.
【解析】
(1)根据题意可以列出相应的二元一次方程组,从而可以解答本题;
(2)根据题意可以列出相应的不等式,从而可以解答本题.
解:(1)设甲商品每件x元,乙商品每件y元,
![]() ,
,
解得,![]() ,
,
即甲商品每件17元,乙商品每件12元;
(2)①设采购甲商品m件,
17m+12(30-m)≤460,
解得,m≤20,
即最多可采购甲商品20件;
②由题意可得,
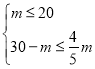 ,
,
解得,![]() ,
,
∴购买方案有四种,
方案一:甲商品20件,乙商品10件,此时花费为:20×17+10×12=460(元),
方案二:甲商品19件,乙商品11件,此时花费为:19×17+11×12=455(元),
方案三:甲商品18件,乙商品12件,此时花费为:18×17+12×12=450(元),
方案四:甲商品17件,乙商品13件,此时花费为:17×17+13×12=445(元).
即购买甲商品17件,乙商品13件时花费最少,最少要用445元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,已知点
 、点
、点 ,动点
,动点 从点
从点 开始在线段
开始在线段 上以每秒
上以每秒 个单位长度的速度向点
个单位长度的速度向点 移动,同时动点
移动,同时动点 从点
从点 开始在线段
开始在线段 上以每秒
上以每秒 个单位长度的速度向点
个单位长度的速度向点 移动,设点
移动,设点 、
、 移动的时间为
移动的时间为 秒.
秒.
 求点
求点 的坐标;
的坐标; 当
当 为何值时,
为何值时, 的面积为
的面积为 个平方单位?
个平方单位? -
科目: 来源: 题型:
查看答案和解析>>【题目】若数a使关于x的分式方程
 的解为正数,且使关于y的不等式组
的解为正数,且使关于y的不等式组 的解集为
的解集为 ,则符合条件的所有整数a的和为()
,则符合条件的所有整数a的和为()A.10B.12C.14D.16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, ,
, 于点E,
于点E, 于点D,BE与AD相交于F.
于点D,BE与AD相交于F. 求证:
求证: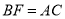 ;
; 若
若 ,求AF的长.
,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数的图象经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是【 】

A.y的最大值小于0 B.当x=0时,y的值大于1
C.当x=-1时,y的值大于1 D.当x=-3时,y的值小于0
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 的顶点为
的顶点为 ,与
,与 轴的一个交点
轴的一个交点 在点
在点 和
和 之间,其部分图象如图所示,则以下结论:①
之间,其部分图象如图所示,则以下结论:① ;②
;② ;③
;③ ;④方程以
;④方程以 有两个的实根,其中正确的个数为( )
有两个的实根,其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.

相关试题

