搜索
【题目】若五个整数由小到大排列后，中位数为4，唯一的众数为2，则这组数据之和的最小值是_____．
参考答案：
【答案】19
【解析】
根据“五个整数由小到大排列后，中位数为4，唯一的众数为2”，可知此组数据的第三个数是4，第一个和第二个数是2，据此可知当第四个数是5，第五个数是6时和最小.
∵中位数为4
∴中间的数为4，
又∵众数是2
∴前两个数是2，
∵众数2是唯一的，
∴第四个和第五个数不能相同，为5和6，
∴当这5个整数分别是2，2，4，5，6时，和最小，最小是2+2+4+5+6=19，故答案为19.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本小题11分）完成下列推理说明：
（1）如图，已知∠1=∠2，∠B=∠C，可推出AB∥CD．理由如下：
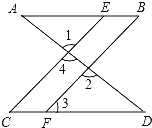
因为∠1=∠2（已知），且∠1=∠4（___________）
所以∠2=∠4（等量代换）
所以CE∥BF（___________）
所以∠___=∠3（_________________）
又因为∠B=∠C（已知）
所以∠3=∠B（等量代换）
所以AB∥CD（______________________））
（2）如图，已知∠B+∠BCD=180°，∠B=∠D．求证：∠E=∠DFE．
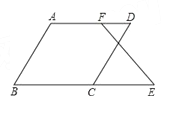
证明：∵∠B+∠BCD=180°（ 已知 ），
∴AB∥CD （__________）
∴∠B= ____（_______________________）
又∵∠B=∠D（ 已知 ），
∴ ∠_____= ∠__________ （ 等量代换 ）
∴AD∥BE（_____________________）
∴∠E=∠DFE（_____________________）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，AD=
AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：①∠AED=∠CED；②AB=HF，③BH=HF；④BC﹣CF=2HE；⑤OE=OD；其中正确结论的序号是_____________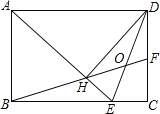
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法中正确的是（ ）
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.每一条边都相等且每一个角也都相等的四边形是正方形
D.平行四边形的对角线相等
-
科目： 来源： 题型：
查看答案和解析>>【题目】不等式3（x-2）≥x+4的解集是( )
A. x≥5B. x≥3C. x≤5D. x≥-5
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知将直线y=x+1向下平移3个单位长度后得到直线y=kx+b，则下列关于直线y=kx+b的说法正确的是（ ）
A.经过第一、二、四象限B.与x轴交于(2，0)
C.与直线y=2x+1平行D.y随的增大而减小
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB=15，BC=14，AC=13，求△ABC的面积．
某学习小组经过合作交流，给出了下面的解题思路，请你按照他们的解题思路完成解答过程．
思路：（1） 作AD⊥BC于D，设BD = x，用含x的代数式表示CD；（2）根据勾股定理，利用AD作为“桥梁”，建立方程模型，求出x；（3）利用勾股定理求出AD的长，再计算三角形面积.
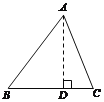
相关试题
