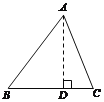
【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
思路:(1) 作AD⊥BC于D,设BD = x,用含x的代数式表示CD;(2)根据勾股定理,利用AD作为“桥梁”,建立方程模型,求出x;(3)利用勾股定理求出AD的长,再计算三角形面积.
参考答案:
【答案】![]() =84.
=84.
【解析】试题分析:(1) 设BD = x ,利用已知条件表示出CD的长即可;(2) 利用勾股定理,在三角形ABD中列出方程,解出即可;(3)利用(2)中的值得出AD的长,利用三角形的面积公式求出面积即可.
试题解析:
(1)如图,在△ABC中,AB=15,BC=14,AC=13,设![]() ,∴
,∴![]() .
.
(2) 由勾股定理得:![]() ,
,![]() ∴
∴![]()
![]() ,
,
解之得:![]() .
.
(3)∵![]() ∴
∴![]() .
.
∴![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若五个整数由小到大排列后,中位数为4,唯一的众数为2,则这组数据之和的最小值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式3(x-2)≥x+4的解集是( )
A. x≥5B. x≥3C. x≤5D. x≥-5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知将直线y=x+1向下平移3个单位长度后得到直线y=kx+b,则下列关于直线y=kx+b的说法正确的是( )
A.经过第一、二、四象限B.与x轴交于(2,0)
C.与直线y=2x+1平行D.y随的增大而减小
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分)
如图,长方形OABC中,O为平面直角坐标系的原点,点A、C的坐标分别为A(3,0)、
C(0,2),点B在第一象限。

(1)写出点B的坐标;
(2)若过点C的直线交长方形的OA边于点D,且把长方形OABC的周长分成2∶3的两部分,求点D的坐标;
(3)如果将(2)中的线段CD向下平移3个单位长度,得到对应线段C′D′,在平面直角坐标系中画出△CD′C′,并求出它的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将
 ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.
ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.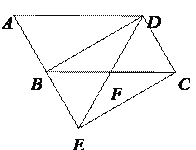
(1)求证:△BEF≌△CDF.
(2)连接BD,CE,若∠BFD=2∠A,求证四边形BECD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )
A.1,2,3B.4,6,8C.6,8,10D.13,14,15
相关试题

